楽しく学ぶ…熱力学
熱力学関数(3) 完全な熱力学関数・マックスウェル関係式
ギブスが基本的な方程式と呼んだ4つの熱力学関数。熱力学ポテンシャルとも言う。
熱力学関数の自然な変数
熱力学関数の数学的な性質については,
積分因子と状態量,
グリーンの定理で説明してきた。
用語も記号もその場に合わせたので, 分かり難くなっている。筆者の頭の整理も含めて, 要約をしておこう。
以下の議論では\(~F(x,y)~\)と\(~F~\)を併記し, 出来るだけ簡潔な表現とする。変数を強調したい場合に\(~F(x,y)~\)を使う。
状態量であるための必要十分条件
熱力学量を2変数の\(~F(x,y)~\)とする。ヘルムホルツの自由エネルギーと紛らわしいが, \(function~\)の\(~F~\)である。
2変数に限ったのは3変数の場合には, 必ずしも積分因子が存在するとは限らないからである。
\(F(x,y)~\)が
\[dF=\dd{F}{x}dx+\dd{F}{y}dy=Pdx+Qdy \]
と表せ,
\[\dd{P}{y}=\dd{Q}{x}\tag{1} \]
を満たす場合に,
(1)\(~dF=0~\)すなわち\(~F(x,y)=Const.~\)なる\(~F(x,y)~\)が存在する。
完全微分方程式となる条件参照。そして,
(2)\(~F(x,y)~\)は積分経路に依らない状態量, すなわち,
\[\int_{A}^{B}F(\bm{r})d\bm{r}=F(B)-F(A) \]
となる, であった。
積分経路に依らない条件参照。
(1)式が成り立たない場合は, 適当な
積分因子\(~\lambda(x,y)~\)(2変数の場合は必ず存在する)を乗じて, \(G(x,y)=\lambda(x,y)F(x,y)~\)とし, \(G(x,y)~\)に同じ操作を加えれば良い。
積分因子の有無に係わらず(1)式が要(かなめ)である。
例えば熱量\(~d'q~\)は
\[\displaystyle d'q=dU+pdV=C_VdT+\frac{nRT}{V}dV\]
\[\dd{C_V}{V}=0,\quad\dd{(nRT/V)}{T}=\frac{nR}{V} \]
で, 状態量では無いが, 積分因子\(~1/T~\)を乗ずると
\[\frac{d'q}{T}=\frac{C_V}{T}dT+\frac{nR}{V}dV\]
\[\dd{(C_VT^{-1})}{V}=\dd{(nR/V)}{T}(=0) \]
となって, 状態量となる。
自然な独立変数 \(Natural\;Variables\)
例えば内部エネルギー\(~U~\)は
\[dU=d'Q+d'W\]
であり, 左辺は完全微分で状態量であるが, 右辺は不完全微分で状態量では無い(過程の量)。(英語圏では次の様に使うようである。The "d' " symbol represent inexact differentials and indicates that both q and w are path functions. Recall that U is a state function.)
これを
\[dU=TdS-pdV \]
とすれば, 両辺とも完全微分で表現出来る(微分方程式論での完全微分はやや異なる)。
この様に, 熱力学関数を全微分であらわすことができる変数をその熱力学関数の「自然な変数」と呼ぶ。
ギブスの基本方程式 完全な熱力学関数
ギブスが基本方程式と呼んだ完全な熱力学関数とは, 系の平衡状態における熱力学的性質の情報を全て持つ示量性状態量のことである。
言葉を換えれば, その関数からは,
全ての状態量を導出できると言うことである。
先ずは, ギブスにより与えられた基本的な方程式を(微分形式で)示そう。導出は容易であるが式変形が延々と続き, 本質を見失う恐れが大きいので割愛した。
\(\qquad\qquad dU=TdS-pdV~\,\: \) 自然な変数は\(~S~\)と\(~V\)
\(\qquad\qquad dF=-SdT-pdV\) 自然な変数は\(~T~\)と\(~V\)
\(\qquad\qquad dH=TdS+Vdp~\; \) 自然な変数は\(~S~\)と\(~p\)
\(\qquad\qquad dG=-SdT+Vdp\) 自然な変数は\(~T~\)と\(~p\)
上記4式はエネルギーに関する関数である。変数の取り方が異なるだけで, 全て
可逆変化に対する熱力学第一法則と等価であり, 熱力学的情報を洩れなく有する。
言い換えれば4つの式は等価であり, 同じ情報を持つ。 数学的には「
ルジャンドル変換」によってサポートされている。
ギブスが何故この4つの量に注目したかは筆者には分からない。
ギブスの自由エネルギーは,
相平衡の満たすべき熱力学関数\(~U(S,V)~\)の平衡曲面の幾何学的条件から導かれた。2変数のルジャンドル変換であるが, ギブスがルジャンドル変換を意識していたかどうかは分からない。
ヘルムホルツの自由エネルギーよりも10年前のことである。エンタルピーなどは定圧下とは言え, ただの熱量ではないか?
ルジャンドル変換の直観的理解 熱力学は話があちらこちらに飛ぶが我慢。
「ルジャンドル変換」が登場したので簡単に説明する。数学的な説明は次節で。
唐突だが内部エネルギー\(~U~\)は, \(S,V~\)を変数として
\[U(S,V)=Ke^{\frac{1}{C_V}(S-RlogV)} \]
と表せる。
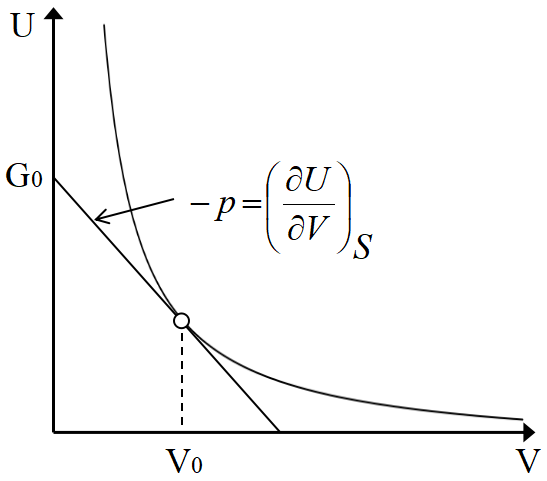
\(S~\)が一定(可逆断熱膨張で実現できる.)で, \(~V=V_0~\)に於いて接線を引いた時, \(U~\)軸の切片が, ギブスの自由エネルギー\(~G_0~\)を表す。
これが\(~U(S,V)~\)から\(~G(T,p)~\)への変数変換で, ルジャンドル変換と呼ぶ。接線の傾き\(~p=-(\partial U/\partial V)_S~\)を新しい変数とするのが特徴である。
\(V~\)一定の時, 同様な接線の傾き\(~T=(\partial U/\partial S)_V~\)があり, \(T,p~\)を新しい変数として\(~U(S,V)\to G(T,p)~\)となる。
平衡曲面の接平面参照。
熱力学ポテンシャル ここから説明が始まる場合も多い。
上記では見通しが良くないので「熱力学的ポテンシャル」と言い換え, 以下の様に記述する場合が多い。
「完全な熱力学関数」という用語もこの辺りから用いられるようである。変数は自然な変数である。
\(\qquad\qquad U=U(S,V)\)
\(\qquad\qquad F=F(T,V)\)
\(\qquad\qquad H=H(S,p)\)
\(\qquad\qquad G=G(T,p)\)
\(F,\;H,\;G~\)については後で述べる。ここではとも角 (カッコ)内の変数を持つ熱力学関数という事にしておこう。
前にも触れたが, ( )内のすっぱいブトー\(~S,p,V,T~\)が自然な変数で, ウガンダハイフン\(~U,G,H,F~\)が熱力学ポテンシャルである。
教科書では\(~U,F,H,G~\)の順での説明が多い。\(~F,H~\)は\(~U~\)から
1回のルジャンドル変換で得られ, \(G~\)では二回必要となるからである。
然し, 歴史的には, \(U(1850)\), \(G(1873)\), \(F(1882)\), \(H(1907)~\)である。エンタルピー\(H~\)はアインシュタインの「奇跡の年」の2年後である。
解析力学のルジャンドル変換は, 一般化座標, 一般化運動量を導入して, 座標依存性の無い運動方程式を導くという目的があった。
熱力学では, 基本方程式を抽出してみたら, それらがお互いに, ルジャンドル変換の形式を満たしていた。という所であろうか。自然の賜物と言えなくもない。
熱力学ポテンシャルの全微分形 ここからが本番。
4つの熱力学的ポテンシャルの全微分を求めると,
\[\begin{align}
&dU=\left(\dd{U}{S}\right)_VdS+\left(\dd{U}{V}\right)_SdV \tag{2}\\
&dF=\left(\dd{F}{V}\right)_TdV+\left(\dd{F}{T}\right)_VdT \tag{3}\\
&dH=\left(\dd{H}{S}\right)_pdS+\left(\dd{H}{p}\right)_Sdp \tag{4}\\
&dG=\left(\dd{G}{p}\right)_Tdp+\left(\dd{G}{T}\right)_pdT \tag{5}
\end{align}\]
を得る。ここで注意すべきは, 例えば内部エネルギーは\(~U(T,V)~\)と書くと完全な熱力学関数とはならないことである。触れておこう。
不自然な変数を選ぶと
\(~U(S,V)~\)の場合。\(S,V~\)以外の状態量\(~T,p~\)は, \(dU=TdS-pdV~\)より
\[\left(\dd{U}{S}\right)_V=T,\quad\left(\dd{U}{V}\right)_S=-p \]
として求まる。これらから\(~S~\)を消去すれば, \(p(V,T)~\)つまり状態方程式が求まる。
一方, \(~U(T,V)~\)の場合,
\[dU=\left(\dd{U}{T}\right)_VdT+\left(\dd{U}{V}\right)_TdV \]
は求まるが, \(p(V,T)~\)つまり状態方程式は求められない。
\(dU=TdS-pdV~\)から\(~p~\)を求めるためには\(~dS=0~\)とする必要があり, \(\displaystyle\left(\dd{U}{V}\right)_T~\)は\(~p~\)ではない。\(~p~\)はあくまでも\(\displaystyle\left(\dd{U}{V}\right)_S~\)である。
さて改めて, 微分形式で表したギブスの基本方程式と(1)~(4)式を比べて次を得る。
\[\begin{align}
&\left(\dd{U}{S}\right)_V=T,\quad\ \left(\dd{U}{V}\right)_S=-p \tag{6}\\
&\left(\dd{F}{V}\right)_T=-p,\;\;\: \left(\dd{F}{T}\right)_V=-S \tag{7}\\
&\left(\dd{H}{S}\right)_p=T,\quad\ \left(\dd{H}{p}\right)_S=V \tag{8}\\
&\left(\dd{G}{p}\right)_T=V,\quad\ \left(\dd{G}{T}\right)_p=-S \tag{9}\\
\end{align}\]
このような対称性をもつ理由は, 各熱力学関数が状態量\(~p,V,T,S~\)のうちのどれか2つを用いれば完全に表される(=独立変数は2個)からである。
一目瞭然であるが(6)~(9)式は,
\[\begin{align}
&\left(\dd{H}{S}\right)_p=\left(\dd{U}{S}\right)_V=T \\
&\left(\dd{G}{T}\right)_p=\left(\dd{F}{T}\right)_V=-S \\
&\left(\dd{U}{V}\right)_S=\left(\dd{F}{V}\right)_T=-p \\
&\left(\dd{H}{p}\right)_S=\left(\dd{G}{p}\right)_T=V
\end{align}\]
と表す場合も多い。式が溢れているが導出の過程は理路整然としているように思える。
マックスウェルの関係式
任意の関数\(~F(x,y)~\)が, その積分経路に依らず, 始点と終点のみで決まるのは, その全微分が完全微分になる事であった。
\[dF=\dd{F}{x}dx+\dd{F}{y}dy=Pdx+Qdy \]
\[\dd{P}{y}=\dd{Q}{x}\tag{10} \]
の時に\(~F(x,y)~\)が保存量, ポテンシャルとなるのである。
(10)式を(2)~(5)式に適用するとどうなるか?内部エネルギー\(~U=U(S,V)~\)でやって見よう。
\[\begin{align}
dU&=\left(\dd{U}{S}\right)_VdS+\left(\dd{U}{V}\right)_SdV \\
&=TdS-pdV
\end{align}\]
に於いて(10)式を当てはめると,
\[\begin{align}
\left[\dd{}{V}\left(\dd{U}{S}\right)_V\right]_S&=\left[\dd{}{S}\left(\dd{U}{V}\right)_S\right]_V\\
\left(\dd{T}{V}\right)_S&=-\left(\dd{p}{S}\right)_V \tag{11}
\end{align}\]
(11)式はマックスウェルの関係式と呼ばれる式の一部である。\(F,H,G~\)についても同様に2階偏導関数を求めて,
\[\left(\dd{S}{V}\right)_T=+\left(\dd{p}{T}\right)_V\tag{12} \]
\[\left(\dd{T}{p}\right)_S=+\left(\dd{V}{S}\right)_p\tag{13} \]
\[\left(\dd{S}{p}\right)_T=-\left(\dd{V}{T}\right)_p\tag{14} \]
を得る。(11)~(14)式がマックスウェルの関係式である。(12)式はエントロピーの体積依存, (14)式はエントロピーの圧力依存を表し, 捉えどころのないエントロピーが, 制御し易い変数\(~T,p,V~\)で実験的に求められる事を示している。
マックスウェルの関係式の応用
ギブスの基本方程式の一つ
\[dU=TdS-pdV \]
より,
\[\begin{align}
\left(\dd{U}{V}\right)_T&=T\left(\dd{S}{V}\right)_T-p \\
&=T\left(\dd{p}{T}\right)_V-p\tag{15} \\
&=T\dd{}{T}\frac{nRT}{V}-p \\
&=T\frac{nR}{V}-\frac{nRT}{V} \\
&=0
\end{align}\]
を得る。1行目から2行目にマックスウェルの関係式の一つ (12) 式を用いた。
温度一定では体積が変化しても内部エネルギー\(~U~\)一定である。つまり\(~U~\)は\(~V,p~\)の関数では無く, 温度\(~T~\)のみの関数である。
ジュール・ゲイリュサックの実験結果が, 熱力学関数から求められた。同様にしてエンタルピーも温度のみの関数であることが示される。
特に(15)式を
エネルギー方程式と呼び, 温度一定のもとでの内部エネルギー\(~U~\)の体積依存性を表す。
シュテファン・ボルツマンの法則の導出に用いられる。
最後の一歩は統計力学が強力である。が, 熱力学は一歩手前の広大な世界を眺めるにはとても適している。