楽しく学ぶ…熱力学
熱力学関数(4) ルジャンドル変換
用語も定義も何とか理解するが, 一体何の役に立つのか分からない。
ルジャンドル変換 \(~Legendre\;Transformation~\)
先ずは具体例から こまかい事は気にしないでやって見よう!
ルジャンドル変換とは関数\(~f(x)~\)から新しい関数
\[g(x)=f(x)-f'(x)x \tag{1} \]
を作りだすことである。
別の言い方では, 変数を\(~x~\)から微分係数\(~f'(x)~\)に変換する(この意味が分かりにくい場合は
切片による1変数ルジャンドル変換参照)ことである。教科書は「作り出す」よりこちらの「変換」の用語が多いが, \(f(x)~\)が残っていて, どこが変換だか分かり難い。
熱力学とどう関係するのか? ヘルムホルツの自由エネルギー\(~F=U-TS~\)を見てみよう。
\[\begin{align}
F&=U-TS \\
&=U-\left(\dd{U}{S}\right)_V S \\
&=U-U' S \tag{2}
\end{align}\]
2行目で\(~\displaystyle T=\left(\dd{U}{S}\right)_V~\)を用いた。
熱力学ポテンシャルの全微分形参照。
(1)式に於いて, \(f(x)\to U,\;x\to S,\; f'(x)\to U' \)とすれば, (2)式は, 関数\(~U~\)から新しい関数\(~F~\)を作る, ルジャンドル変換である。
\(F~\)は\(~U~\)から一回のルジャンドル変換で得られる。
別の例を見てみよう。エンタルピー\(~H=U+pV~\)は,
\[\begin{align}
H&=U+pV \\
&=U-\left(\dd{U}{V}\right)_S V \\
&=U-U' V
\end{align}\]
\(~\displaystyle -p=\left(\dd{U}{V}\right)_S~\)を用いた。
\(f(x)\to U,\;x\to V,\; f'(x)\to U'~\)とすれば\(~H=U+pV~\)は関数\(~U~\)から新しい関数\(~H~\)を作る, ルジャンドル変換である。
\(H~\)も\(~U~\)から一回のルジャンドル変換で得られる。
熱力学においてルジャンドル変換はありふれたものである。「ルジャンドル変換とは, 変数を入替えて次々と熱力学関数を作り出すこと」という説明もあながち間違ってはいない。然し, 何故わざわざ○○変換などと大袈裟な名前を付けるのだろうか?ただの式変形ではないか?と思ってしまうが。
固有名詞で呼ぶ理由は,
ルジャンドル変換された状態量同士では, 情報の欠落は無い事が保証されているからである。
情報の欠落を起こす変換 不用意に変数の変換をすると!
\(~a~\)を定数として
\[f(x)=(x−a)^2 \]
という関数を考える。今は\(~x\to f(x)~\)という関数になっているわけだが, 新しい変数として\(~f~\)の\(~x~\)による微分,
\[p_x=\partial f/\partial x=2(x−a)\]
を取るとする。逆に, \(x=p_x/2+a~\)である。微分係数\(~p_x~\)を変数として\(~f~\)を表現すると,
\[f=\frac{(p_x)^2}{4} \]
である。結果は\(~a~\)によらない式になった。つまり\(~a~\)という情報が欠落してしまった。
それに対して, ルジャンドル変換は, 逆変換で元に戻すことのできる, 完全な変換の一つである。
切片による1変数ルジャンドル変換
(1)式による定義は図形的な意味が分かり難いので, 新しい定義を採用する。2つの定義が同値であるのは直ぐに分かるので心配は要らない。
定義:関数\(~f(x)~\)に対して\(~\displaystyle g(p)=\max_{x} \{px−f(x)\}~\)で定義される関数\(~g(p)~\)を\(~f(x)~\)のルジャンドル変換と呼ぶ。
実際の応用例では\(~f~\)側の変数と\(~g~\)側の変数は違う意味を持つ量なので, \(~f~\)側の変数は文字\(~x~\), \(~g~\)側の変数は文字\(~p~\)を用いる場合が多い。
(例題)
二次関数\(~f(x)=ax^2 (a>0)~\)をルジャンドル変換せよ。
(解答)
\[\begin{align}
g(p)&=\max_{x}\{px−f(x)\} \\
&=\max_{x}\{px−ax^2\} \\
&=\max_{x}\left\{-a\left(x-\frac{p}{2a}\right)^2+\frac{p^2}{4a} \right\} \\
&=\frac{p^2}{4a}\tag{3}
\end{align}\]
つまり原点を頂点とする放物線のルジャンドル変換は, 原点を頂点とする放物線である。
変数が\(~x~\)から\(~p~\)に変わっていることに注意。
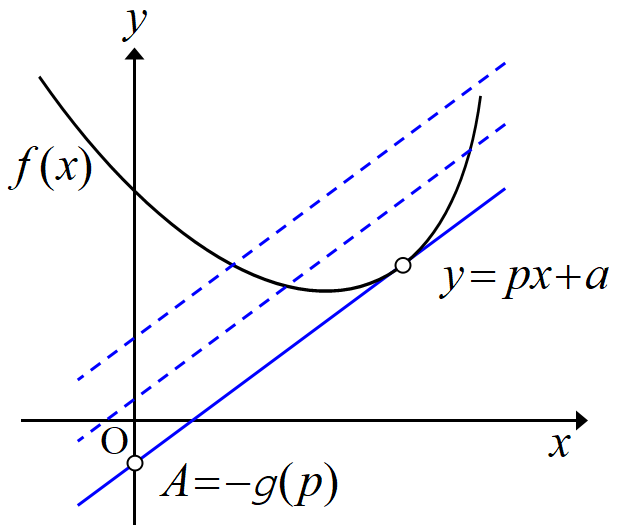
意味が分かりにくいが, 図を見た方が早い。複雑さを避け, ここからは\(~f(x)~\)が下に凸な場合を考える。
\(~f(x)~\)のルジャンドル変換された関数\(~\displaystyle g(p)=\max_{x}\{px−f(x)\}~\)は, 図の\(~\rm A~\)点に対応する。
傾き\(~p~\)の直線で\(~f(x)~\)と交わるものの中で一番下側にあるもの, すなわち曲線\(~y=f(x)~\)の接線の切片にマイナスをつけたものである。
(証明)
傾き\(~p~\)の\(~f(x)~\)との接線の切片を\(~A~\)とおくと,
\[\min_{x} \{f(x)-(px+A)\}=0~\]
である。移項して,
\[-A=-\min_{x} \{f(x)-px\}=\max_{x} \{px-f(x)\}\]
を得る。(証明終わり)
ルジャンドル逆変換 ルジャンドル変換は完全な変換。
ここで上記で得られた\(~g(p)~\)をもう一度ルジャンドル変換して見よう。
(例題・逆変換)
二次関数\(~\displaystyle g(p)=\frac{p^2}{4a}~\)をルジャンドル変換せよ。
(解答・逆変換)
\[\begin{align}
h(x)&=\max_{p}\{xp−g(p)\} \\
&=\max_{p}\left\{xp−\frac{p^2}{4a}\right\} \\
&=\max_{p}\left\{-\frac{1}{4a}(p-2ax)^2+\frac{1}{4a}(4a^2x^2)\right\} \\
&=ax^2
\end{align}\]
となり, 元に戻る。つまり逆変換が可能で, (4)式の様に情報は失われていない。
これは偶然ではなく, 一般に, 下に凸な関数\(~f(x)~\)に対して2回ルジャンドル変換を施すと元に戻る。下に凸でないと, こう上手くは行かない。
下に凸と限定すれば, 定義式\(~\displaystyle g(p)=\max_{x}\{px−f(x)\}~\)の\(~max~\)は取り外せて,
\[g(x)=f(x)-px=f(x)-f'(x)x \]
となり, (1)式と同じ結果を得る。
詳細な証明は省略した。深く知りたい読者は「ルジャンドル変換とは, 多様体上での座標変換である」等で検索し, 勉強されたし。
結局ルジャンドル変換とは同じ曲線を,
「\(x,\;y~\)座標で,(従来通り)\(~x,f(x)~\)で表現する」代わりに「接線の傾き\(~f'(x)\), 切片\(~−g(x)~\)で表現した」ものと見ることが出来る。
つまり, \(f(x)~\)の包絡線を求めることである。包絡線とはどのような物か? 見てみよう。
\(f(x)=x^2~\)上の点\(~(t,t^2)~\)における接線の方程式は, \(f'(t)=2t~\)より,
\[\begin{align}
y-t^2&=2t(x-t) \\
y&=px-\frac{p^2}{4}\quad (~p=2t) \\
g(p)&=-\left(-\frac{p^2}{4}\right)=\frac{p^2}{4}
\end{align} \]
\(g(p)~\)が,
接線の傾き\(~p~\)を新しい変数とした, ルジャンドル変換された関数である。(切片ではなく, ーをつける.)
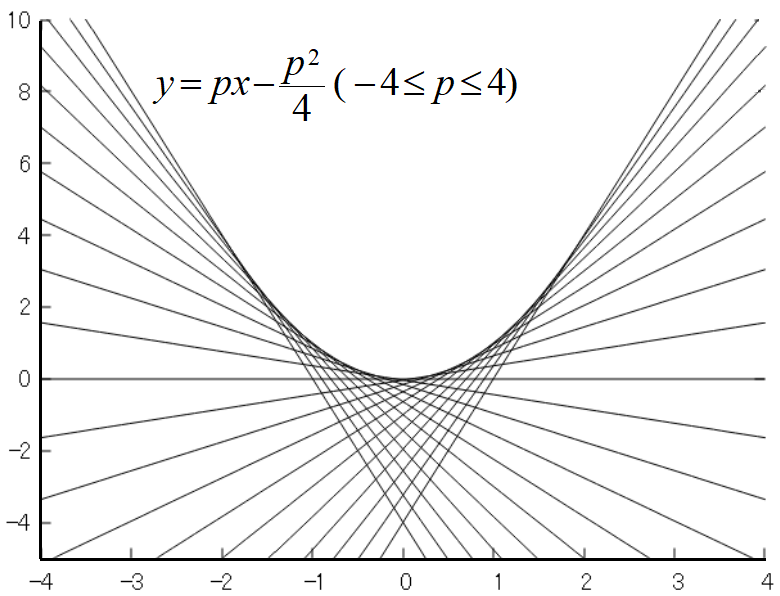
図は, \(y=px-p^2/4~\)に於いて, \(~p=-4.0\to +4.0~\)まで\(~0.4~\)刻みでプロットした
包絡線である。
\(g(p)~\)は, 元の関数\(~f(x)=x^2~\)の情報を漏れなく持っている事が容易に推察される。
図形的にも関数の凸性が必要なことが分かる。凸でないと(部分的に凹んでいること)包絡線が描けないことは明らかであろう。
2変数ルジャンドル変換 熱力学関数は2変数である。
多くの教科書では, 以上で説明は終わりである。しかし目的も, 具体的な使い方も分らない。次々と式変形するのが目的ではなかろう。
前に「ルジャンドル変換は状態量同士で情報の欠落が無い事を保証」と書いた。数学的にはその通りであるが, 熱力学においては少々異なる気がしている。
それは
多相平衡と自由エネルギーの密接な関係がルジャンドル変換だった, という事である。
熱力学は熱機関を離れ, 宇宙の森羅万象を記述する熱力学へと進化を遂げた。その進化を支えたのがルジャンドル変換である。
熱力学は基本的に2変数であるので, 2変数ルジャンドル変換の方が真価を発揮する。
ギブスが認識していたかどうかは不明だが, ギブスが自由エネルギーを導出した過程は正にルジャンドル変換である。
熱力学関数の幾何学(2) 自由エネルギー参照。
ここでは数学の演習として, 2変数のルジャンドル変換を行ってみよう。
直感的には切片(にーをつける)の方が分かりやすいが, 計算は(1)式, \(g(x)=f(x)-f'(x)x~\)の方が扱いやすい。
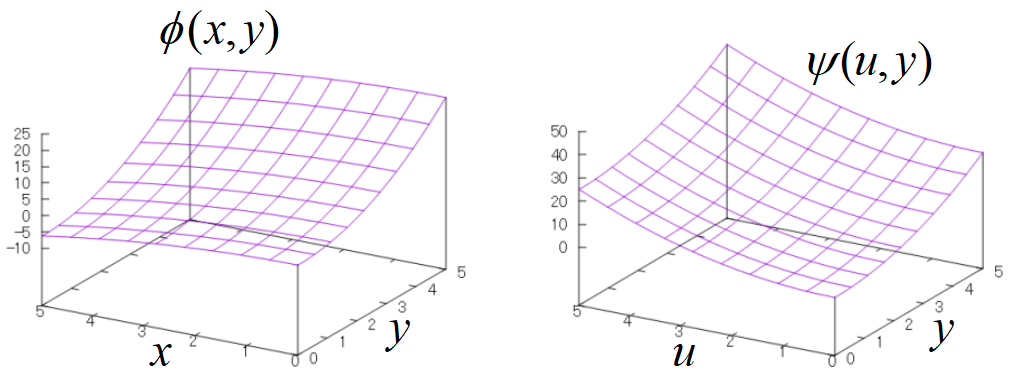
\(\phi(x,y)=x^2+2y^2~\)の全微分を取って,
\[\begin{align}
d\phi(x,y)&=\left(\dd{\phi}{x}\right)dx+\left(\dd{\phi}{y}\right)dy \\
&=2xdx+4ydy \\
&=udx+vdy \\
x&=\frac{u}{2},\;y=\frac{v}{4}
\end{align}\]
\(~u,\;v~\)を変数とする新しい関数を作る訳である。
先ず, \(y~\)を一定にして, \(~x\to u~\)にした新しい関数\(~\psi(u,y)~\)を作る。(1)式に当てはめて,
\[\begin{align}
\psi(u,y)&=\phi(x,y)-ux \\
&=\left(\frac{u}{2}\right)^2+y^2-u\frac{u}{2} \\
&=-\frac{u^2}{4}+y^2
\end{align}\]
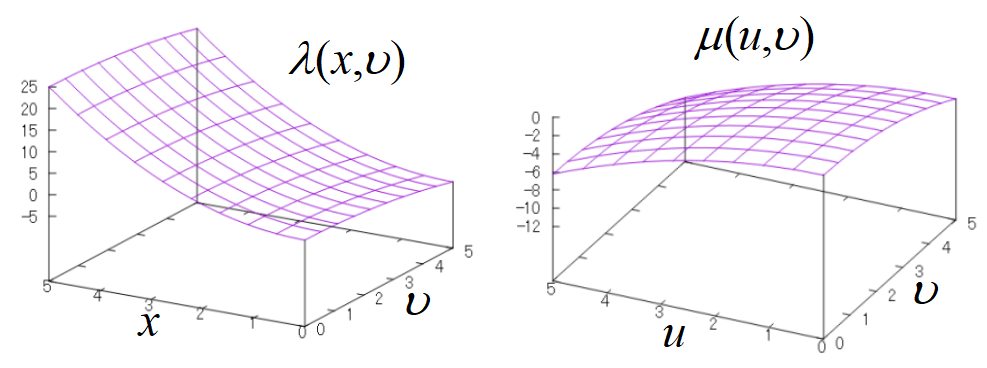
次に\(y~\)を一定にして\(~y\to v~\)にした新しい関数\(~\lambda(x,u)~\)を作る。(1)式に当てはめて,
\[\begin{align}
\lambda(x,v)&=\phi(x,y)-vy \\
&=x^2+\left(\frac{v}{4}\right)^2-v\frac{v}{4} \\
&=x^2-\frac{3}{16}v^2
\end{align}\]
最後に\(~x\to u,\;y \to v~\)にした新しい関数\(~\mu(u,v)~\)を\(~\psi(u,y)~\)から作る。(1)式に当てはめて,
\[\begin{align}
\mu(u,v)&=\psi(u,y)-vy \\
&=-\frac{u^2}{4}+\left(\frac{v}{4}\right)^2-v\frac{v}{4} \\
&=-\frac{1}{4}u^2-\frac{3}{16}v^2
\end{align}\]
同じことであるが, \(~\mu(u,v)~\)は\(~\lambda(x,u)~\)からも作る事が出来て,
\[\begin{align}
\mu(u,v)&=\lambda(x,v)-ux \\
&=-\frac{3}{16}v^2+\left(\frac{u}{2}\right)^2-u\frac{u}{2} \\
&=-\frac{1}{4}u^2-\frac{3}{16}v^2
\end{align}\]
としても良い。あるいは2変数の場合は, \(\phi(x,y)~\)から\(~x\to u,\;y \to v~\)を一気に進めるのが速い。
\[\begin{align}
\mu(u,v)&=\phi(x,y)-ux-vy \\
&=\left(\frac{u}{2}\right)^2+\left(\frac{v}{4}\right)^2-u\frac{u}{2}
-v\frac{v}{4} \\
&=-\frac{1}{4}u^2-\frac{3}{16}v^2
\end{align}\]
\(\displaystyle \mu(u,v)=-\frac{1}{4}u^2-\frac{3}{16}v^2 ~\)が\(~\phi(x,y)=x^2+2y^2~\)のルジャンドル変換である。
ルジャンドル変換では, 曲線が曲線に移り, 曲面が曲面に移る。
\(~\phi(x,y),\;\psi(u,y),\;\lambda(x,v),\;\mu(u,v)~\)のグラフを示す。
φは下に凸な関数, μは上に凸な関数となっている。