楽しく学ぶ…熱力学
内部エネルギー・比熱・エネルギー方程式
クラウジウスはある形態のエネルギー\(~U~\)が
見えない所に隠されていることを突き止めた。1850年26歳の時である。
定積比熱と定圧比熱 定積比熱は定積過程だけではなく, 定圧過程にも適用でき, 熱力学一般に広く用いられる。
再び熱力学第一法則 \(\varDelta U=C_V\varDelta T~\)は体積一定でなくとも使う。
熱力学第一法則を再掲しよう。気体の場合\(~-W=-p\varDelta V~\)を使って
\[\varDelta U=\varDelta Q -p\varDelta V \]
定積過程では, 系は外界に対して仕事をしない(膨張出来ないので, 仕事も出来ない)。
\(\varDelta V=0\)だから\(~\varDelta U=\varDelta Q=C_V\varDelta T\)。\(C_V~\)を「定積比熱」と呼ぶ。\(C_V~\)を1モル当たりの値とすれば, \(n~\)モルの気体では
\[\varDelta U=n\;C_V\varDelta T\tag{1} \]
である。高温熱源から得た熱は, 全て系の温度を上げるために使われ, 内部エネルギーの増加となる。
ここで注意すべきは, (1)式は
定積過程でなくとも定圧過程でも使って良いことである。
内部エネルギー\(~\varDelta U~\)は\(~\varDelta U=C_V\varDelta T~\)と定義されるとしても良い。
熱力学はここまでで, \(C_V~\)の温度依存性, ひいては内部エネルギーの温度依存性は分からない。新しい事実が必要である。
定積比熱\(~C_V~\)と定圧比熱\(~C_p~\) マイヤーの関係式
マイヤーの関係式は, 理想気体でない場合は
\(Mayer~\)サイクル, あるいは
熱力学関数の演算 によって求める。(その方がカッコ良いが), 理想気体の場合は, 現象をよく考えれば簡単に求まる。特に受験生は注意されたい。出題者も難しい計算よりも, 本質を理解している方を望むのではないか?
以下は全て理想気体1モルについての議論である。
定圧過程の場合も同様にして, 定圧比熱\(~C_p~\)を定義する。定積過程では系は外界に対して仕事をしないので, 高温熱源から得た熱は, 全て内部エネルギーの増加となる。
\[\varDelta Q_V=C_V\varDelta T=\varDelta U\]
一方定圧過程では, 高温熱源から得た熱は系の温度を上げて内部エネルギーを増加させると共に, 外界に対して仕事を行う。
\[\varDelta Q_p=C_p\varDelta T=\varDelta U+p\varDelta V\]
2つの過程で, 系を
同じ温度\(~\varDelta T~\)だけ上げるためには, \(~\varDelta Q_p~\)は\(~\varDelta Q_V~\)より仕事分\(~p\varDelta V~\)だけ多く必要となる。
\(pV=nRT~\)より1モルあたり, \(p\varDelta V=R\varDelta T\)だから,
\[\varDelta Q_p=C_V\varDelta T+ R\varDelta T=(C_V+R)\varDelta T= C_p\varDelta T\]
であり, 気体1モルに対して
\[C_p=C_V+R \tag{2} \]
である。(2)式を「マイヤーの関係式」と呼ぶ。
マイヤーはジュールに先立って, 熱の仕事当量を算出した。熱力学建設の功労者である。
断熱関係式 等温過程では\(~pV=\)一定。断熱過程では\(~pV^{\gamma}=\)一定。
断熱過程では\(~\varDelta Q=0~\)より, 理想気体 1 モルに対して,
\[\begin{align}
\varDelta U+p\varDelta V&=C_V\varDelta T+\frac{RT}{V}\varDelta V=0 \\
\frac{\varDelta T}{T}+\frac{R}{C_V}\frac{\varDelta V}{V}&=0 \\
logT+\frac{R}{C_V}logV&=logTV^{\frac{R}{C_V}}=C \\
\frac{pV}{R}\cdot V^{\frac{R}{C_V}}&=\frac{1}{R}pV^{1+\frac{R}{C_V}}=\frac{1}{R}pV^{\frac{C_V+R}{C_V}}=C \\
pV^{\frac{C_P}{C_V}}&=pV^{\gamma}=C \tag{3}
\end{align}\]
を得る。定数\(~C~\)は全て異なるので注意。最後の行でマイヤーの関係式\(~C_p=C_V+R\), 断熱定数\(~\gamma=C_p/C_V~\)を用いた。
これを
ポアッソンの関係式と呼ぶ。
内部エネルギーの変数 高校物理では\(~\displaystyle U=\frac{3}{2}nRT~\)と習ったが。
ジュール・ゲイリュサックの実験
ゲイリュサックが1809年に, 精度を上げてジュールが1845年に行った実験は, 内部エネルギーが温度のみの関数であることを示唆していた。
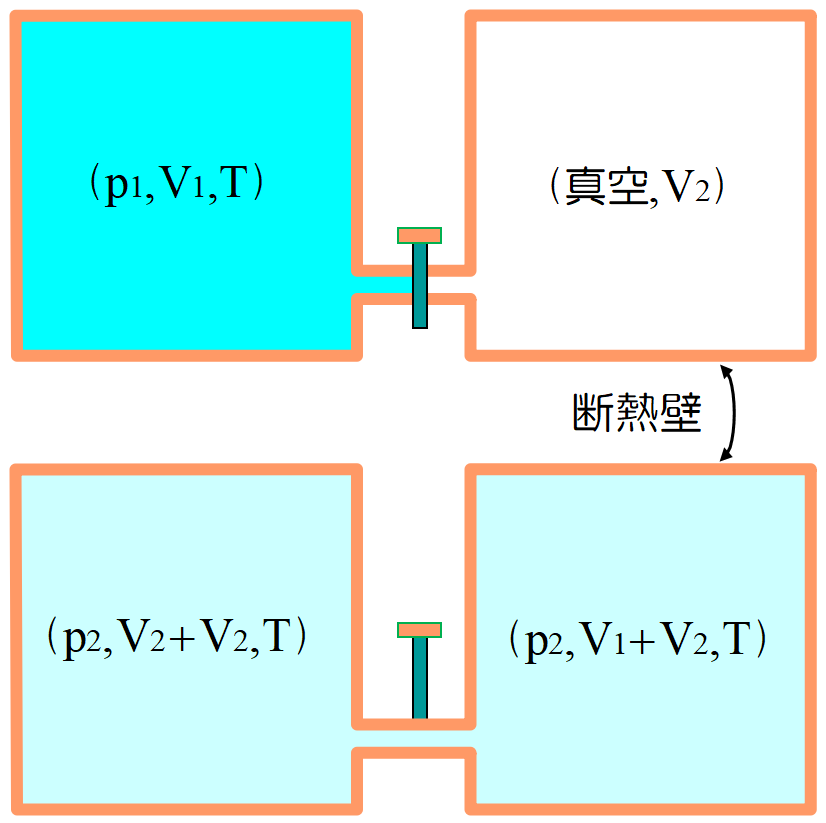
2つの断熱容器の片方(体積\(~V_1~\))に気体を満たし, もう一方(体積\(~V_2~\))は真空にしておく。その間にあるコックを開放すると, 気体は不可逆的に両方の容器一杯に広がる。真空に拡がる自由膨張なので仕事はせず, また断熱操作なので内部エネルギーに変化は無い。この一様に広がった気体の温度を測定する。2人の実験結果は一致し, 温度変化は\(~\varDelta T=0~\)というものであった。電流のジュール熱と紛らわしいが, ジュールの法則と呼ぶ。
特にジュールの実験精度は高く, 0.056℃未満の誤差で測定した。ジュールはその生涯を熱量の測定に捧げ, 誰にも反論できない事実を積み上げていった。それだからこそ, トムソン(ケルビン)もクラウジウスも安心して自説を展開出来た。
高電圧の電池で自分や召使の少女に電気ショックを与えて, 少女を失神させてしまったとか, 新婚旅行先で花嫁はそっちのけで, 滝の上と下で\(~mgh~\)の分, 水温が上がることを確かめようとしたとかの類の話は枚挙にいとまがない。もっとも後者はトムソン(ケルビン)の創作らしいが。それだけ親しかったということか!
内部エネルギーは温度のみの関数
さて内部エネルギーの変数だが, \(\varDelta T=0~\)の実験結果さえ認めれば, 数式は無くとも説明は可能である。
明らかに内部エネルギーの変化はゼロである。\(\varDelta U=0~\)。体積は変化\(~V_1\to V_1+V_2~\)しているので, \(U~\)は体積\(~V~\)の関数では無い。
温度 \(~T~\)は変化していない(実験結果)ので, \(pV=~\)一定より, \(p~\)も変化している。すなわち\(U~\)は圧力\(~p~\)の関数でも無い。(圧力\(~p~\)に関しては敢えて言及する必要はないが, 気になる読者もおられると思うので記述した.)
以上より内部エネルギー\(~U~\)は体積\(~V~\)に依存せず(当然, 圧力\(~p~\)にも依存しない), 温度\(~T~\)に依存するしかない。すなわち温度のみの関数である。
しかし, これでは「それらしく」無いので, 計算で示そう。
内部エネルギーの熱力学的証明(1) エネルギー方程式
状態関数(熱力学関数)からは実に多くの関係式が導かれる。
完全な熱力学関数の一つ, ヘルムホルツの自由エネルギー\(~F=U-TS~\)からは
\[\left(\dd{F}{T}\right)_V=-S,\quad\left(\dd{F}{V}\right)_T=-p\]
が導かれ, さらに, \(U=TS+F~\)を\(~V~\)で微分し,
マックスウェルの関係式の一つ\(~\displaystyle \left(\dd{S}{V}\right)_T=-\left(\dd{p}{T}\right)_V~\)を使えば,
\[\begin{align}
\left(\dd{U}{V}\right)_T&=T\left(\dd{S}{V}\right)_T+\left(\dd{F}{V}\right)_T\\
&=T\left(\dd{p}{T}\right)_V-p \tag{5}
\end{align} \]
という関係が得られる。(5)式を
エネルギー方程式と呼ぶ。
理想気体\(~pV=nRT~\)にこの式を適用すると,
\[\left(\dd{U}{V}\right)_T=T\dd{}{T}\left(\frac{nRT}{V}\right)-\frac{nRT}{V}=0 \]
以上より, 内部エネルギー\(~U~\)は体積\(~V~\)に依存せず(当然, 圧力\(~p~\)にも依存しない), 温度\(~T~\)のみの関数である。
マックスウェルの関係式の応用に他の導き方を示す。教科書はこちらが多い様である。
熱力学はここが限界である。\(U~\)が, \(U=k_1T~\)なのか, \(U=k_2T^2~\)なのかその形を決めることは出来ない。統計力学の応援が必要である。
まぁ, \(~\displaystyle U=\frac{3}{2}nRT~\)の方が分かり易いと言えば分かり易いが。
電磁場と熱力学 シュテファン・ボルツマンの法則
エネルギー方程式の応用例として, 平衡状態の真空中の電磁場の問題を見てみよう。
統計力学から導こうとしたときの圧倒的な困難さが, 量子力学誕生のきっかけになった。
電磁場のエネルギー密度と圧力の間には,
\[p=\frac{1}{3}u \]
の関係がある。この電磁場のエネルギー密度と温度の関係を考えてみよう。(5)式導出と重複するがやってみよう。
\[dU=TdS-pdV \]
である。両辺を温度一定の条件で\(~dV~\)で割ると, 左辺\(~\displaystyle \left(\dd{U}{V}\right)_T~\)はエネルギー密度であるから,
\[u=T\left(\dd{S}{V}\right)_T-p \]
ここでマクスウェルの関係式,
\[\left(\dd{S}{V}\right)_T=-\left(\dd{p}{T}\right)_V \]
を使うと,
\[u=T\left(\dd{p}{T}\right)_V-p \]
となる。(5)式エネルギー方程式である。\(p=u/3~\)を代入して,
\[u=\frac{T}{3}\left(\dd{u}{T}\right)_V-\frac{u}{3} \]
を得る。あとは変数分離で普通に積分して,
\[\begin{align}
\frac{4}{3}u&=\frac{T}{3}\left(\dd{u}{T}\right)_V \\
\frac{1}{u}du&=\frac{4}{T}dT \\
log\,u&=4log\,T+C \\
u&=aT^4
\end{align} \]
となる。定数は熱力学の範囲では求められないが, 4乗の部分は簡単に求まる。
熱輻射により黒体から放出されるエネルギー密度が\(~T^4~\)に比例するシュテファン・ボルツマンの法則が得られた。
エントロピーもマックスウェルの関係式もまだ出てきていないが, このように話があちらこちらに飛ぶのも熱力学の特徴である。
熱力学は, 力学, 電磁気学のように階層的に組みあがっているのではなく, 全体として一つにまとまっている個体のような感じがする。
付録\(\quad Mayer~\)サイクル 受験正専用熱サイクルだが。
熱サイクルを考える時, 最も基本的な等温過程での仕事は, 積分操作が避けられず現在の高校物理では取り扱えない。
断熱過程では積分を用いなくとも内部エネルギー(温度のみの関数)で仕事を計算できる。よって等温過程抜きの熱サイクルは高校教科書, 入試問題では良く取り上げられる。熱力学の教科書では, 敢えて変則的なサイクルは取り上げる必要はなく, ほとんど見ることは無い。しかし受験生には必要なので取り上げてみた。
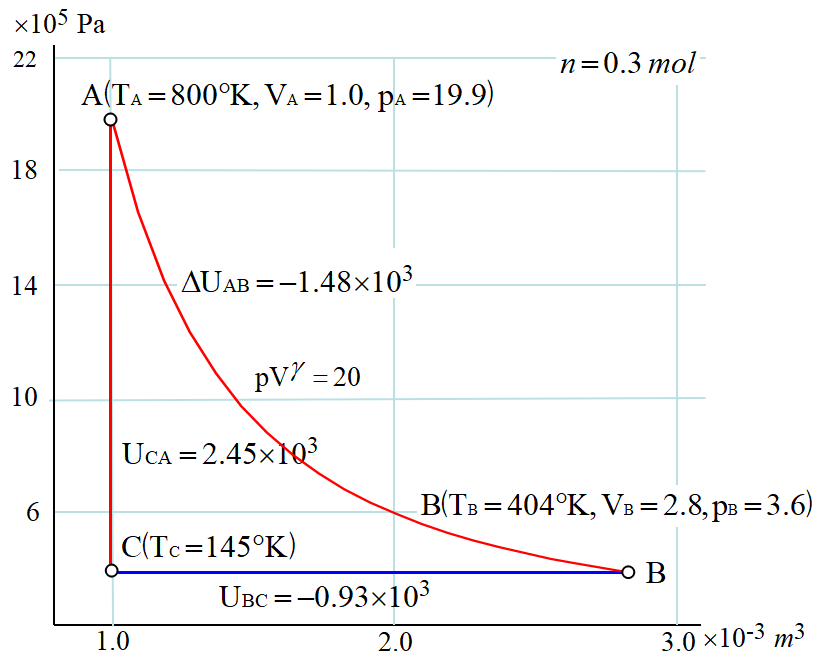
\(A \to B~\)は断熱膨張過程, \(B \to C~\)は等圧圧縮過程, \(C \to A~\)は等積(加熱)過程である。
各過程での内部エネルギーの変化を求めると,
\[\begin{align}
\varDelta U_{A \to B}&=C_V \varDelta T=\frac{C_V}{R}(p_BV_B-p_AV_A) \\
\varDelta U_{B \to C}&=\varDelta Q-p\varDelta V \\
&=C_p\varDelta T-p_B(V_C-V_B) \\
&=\frac{C_p}{R}(p_CV_C-p_BV_B)-p_B(V_C-V_B) \\
&=\left(\frac{C_p}{R}-1\right)p_B(V_C-V_B) \\
\varDelta U_{C \to A}&=C_V \varDelta T=\frac{C_V}{R}(p_AV_A-p_CV_C)
\end{align}\]
上から5番目の式は\(~p_B=p_C~\)を用いた。すべてを足し合わせると\(~A \to A~\)の内部エネルギーの変化となるので明らかに0。
\[\begin{align}
\varDelta U_{A \to B}+\varDelta U_{B \to C}+\varDelta U_{C \to A}
&=\frac{C_V}{R}(p_BV_B-p_AV_A)+\left(\frac{C_p}{R}-1\right)p_B(V_C-V_B)
+\frac{C_V}{R}(p_AV_A-p_CV_C)\\
&=\frac{p_B}{R}(V_A-V_B)(C_p-C_V-R)=0
\end{align}\]
\(V_1\neq V_2~\)より
\[C_p-C_V=R \tag{6} \]
これが\(~Mayer~\)の式と呼ばれる。因みに図の場合,
\[\begin{align}
U_{A\to B}&=nC_V\varDelta T=3/2\x 0.3\x 8.314(404-800)=-1.48\x10^3 \\
U_{B\to C}&=nC_P\varDelta T+P_B(V_B-V_A)=5/2\x 0.3\x 8.314(145-404)+3.6\x 10^5(2.8-
1.0)\x 10^{-3} \\
&=-1615+684=-0.93\x 10^3 \\
U_{C\to A}&=nC_V\varDelta T=3/2\x 0.3\x 8.314(800-145)=2.45\x 10^3
\end{align}\]
より,
\[-1.48-0.93+2.45=0.04\x 10^3\; [J]\]
となる。\(\rm B\to \rm C~\)の圧縮過程でさえ内部エネルギーは減少する。
ガスタービンエンジンは断熱膨張でエネルギーを取り出すらしい。大量の熱(燃料)を取り込んで圧縮し, 急膨張させて出力する。
サイクル動作は不要だから, 図の例でいえば熱効率は\(~\eta=1.48/2.45=60\;\%~\)でかなり高い。(圧縮機の駆動は考慮していません)。けれども, 精緻な理論には使えそうもない。
トムソン(ケルビン卿)が絶対温度を導き, クラウジウスがエントロピーを発見したカルノーサイクルは本当に良く出来ている!