楽しく学ぶ…熱力学
熱力学関数(1) 状態量・ベクトル場の線績分
ある条件を満たすベクトル場の戦績分は経路によらない状態量となる。
状態量 経路によらない物理量とは?
平衡状態を一つ決めれば値が確定する物理量を状態量または熱力学関数と言う。
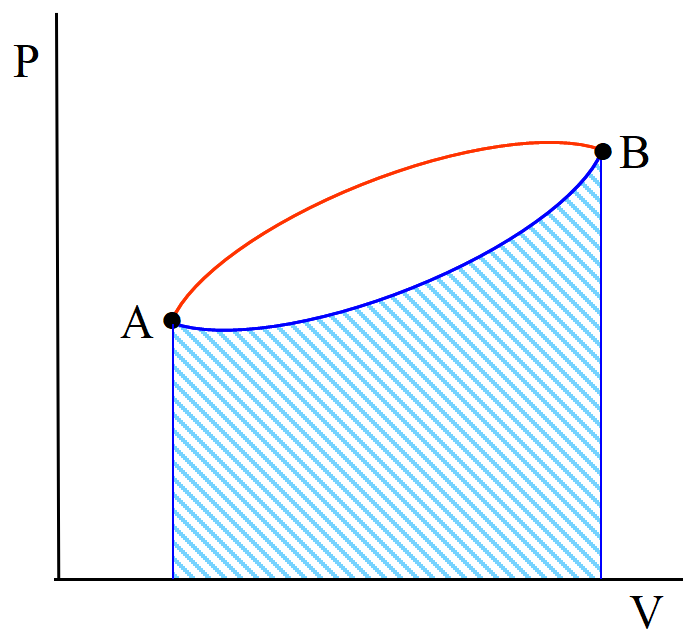
(1) 仕事は状態量では無い。
\(\rm A\to B~\)において, 青線に沿った仕事量は青斜線部分である。青線と赤線では仕事が異なり, \(B~\)という状態が確定しても, 仕事量は定まらない。
(2) 熱量は状態量では無い。
こちらはそんなに自明ではない。実例を挙げよう。
\(0^{\circ}\rm C\), 1 気圧の気体を\(~100^{\circ}\rm C\), 10 気圧にする。1 気圧に保って\(~100^{\circ}\rm C~\)まで熱し次に温度を一定に保って10気圧に圧縮する場合と, \(0^{\circ}\rm C~\)の下で等温的に10気圧まで圧縮してその後定圧的に\(~100^{\circ}\rm C~\)まで加熱した場合で加えるべき熱量は全く異なる。
これに対し, 状態量はその状態に至る経路に依らない量であり, 一般的には重要な物理量である事が多い。
熱力学では, 熱平衡状態を指定すれば,唯一定まるこの状態量\(~quantity\;of\;state~\)を
熱力学関数と呼ぶ。理想気体の場合で言えば, \(S,P,V,T,U,G,H,F~\)であり, 微小量を\(~dS,dP,\dots,dF~\)で表す。(すっぱいブトー, ウガンダハイフンと言うらしい.)すっぱいブトーが状態量変数, ウガンダハイフンが熱力学ポテンシャルである。
一方, 熱平衡状態を動かすための量\(~quantity\;of\;process~\)を
過程の量と呼ぶ。\(W,Q~\)であり, 微小量を\(~d'W, d'Q~\)で表す。
上記の状態量は全て熱力学関数であるが, ギブスが基本的な方程式と呼んだ, 特別な熱力学関数がある。\(~U(S,V),\;G(T,p),\;H(S,p),\;F(T,V)~\),\(S(U,V)~\)である。現代では
完全な熱力関数と呼ぶ。最後の\(~S(U,V)~\)は含めない場合もあるようである。
完全な熱力学関数とは, 熱力学ポテンシャルとも呼ばれ, 熱力学的性質の情報を全て持つ示量性状態量である。別の言い方をすると, その関数から他の全ての熱力学的状態量を導き出せる関数である。
そして, 思わず「どうして?」と叫びたくなるほど, その数学的構造に見とれてしまう。順次進もう!
多変数関数の微積分 熱力学が驚くほど上手くできているのは変数が2つだから。
偏微分 熟知している読者は次の「グリーンの定理」へ。
二変数関数\(~f(x,y)~\)の\(~x~\)方向に関する偏微分は
\[\dd{f(x,y)}{x}=\lim_{\varDelta x \to 0}\frac{f(x+\varDelta x)-f(x)}{\varDelta x} \]
\(y~\)を個定して, \(x~\)で通常の微分をすれば良い。
図での\(\displaystyle \dd{f(x,y)}{x}\)は, 点\(~(x,y)~\)に於ける山の斜面の\(~+x~\)方向の傾きである。例として\(~f(x,y)=x^2y~\)の時, その偏微分は
\[\dd{f(x,y)}{x}=2xy,\quad \dd{f(x,y)}{y}=x^2 \]
である。
勾配と全微分
全微分については以前にも触れた。点\(~(x,y)~\)に於ける関数\(~f(x,y)~\)の\(~x,y~\)方向の傾きを, まとめてベクトルで
\[\nabla f(x,y)=\left(\dd{f(x,y)}{x},\dd{f(x,y)}{y}\right)\tag{1} \]
と表す。\(\nabla~\)(ナブラ)は,
\[\nabla=\left(\dd{}{x},\dd{}{y}\right)=\dd{}{x}\bm{i}+\dd{}{y}\bm{j}\]
のベクトル演算子である。(1)式は\(~\nabla f~\)とも書かれ, 幾何学的には高度\(~f(x,y)~\)を持つ山の, 位置\(~(x,y)~\)における勾配を表す。
勾配\(~\nabla f~\)を用いると, 位置\(~(x,y)~\)から\(~x+\varDelta x,y+\varDelta y~\)へと微小移動した際の, 高さ\(~"f"~\)の変化\(~df~\)が, 微小移動ベクトル
\[d\bm{r}=(dx,dy) \]
と勾配 (1) を用いて,
\[df=\nabla f\cdot \bm{r}=\dd{f(x,y)}{x}dx+\dd{f(x,y)}{y}dy\tag{2} \]
と表せる。すなわち微小移動に際しての高度の変化\(~df~\)は, 勾配\(~\nabla f~\)と移動ベクトル\(~d\bm{r}~\)のとの内積に等しい。
この\(~df~\)を
全微分と呼ぶ。特に等高線に沿った微小移動\(~d\bm{r}~\)では高度が変化しない(\(~df=0~\))ので\(~\nabla f\cdot d\bm{r}=0~\)が成り立つ。
つまり
勾配ベクトル\(~\nabla f~\)は等高線に垂直である。
線積分 スカラー量を扱う熱力学でもベクトル場の線積分が主役。
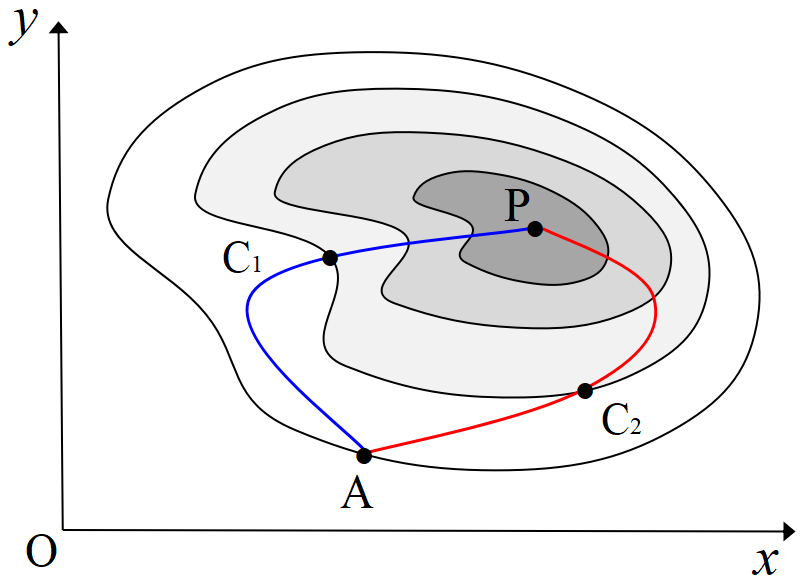
前の図で, 点\(~A~\)から頂上\(~P~\)まで登山道\(~C_1~\)に沿って登るとする。その際に歩いた距離や上った高さは, 経路\(~C_1~\)に沿って微小な長さや高さを足し上げる, つまり積分することによって求められる。一般に, ある経路に沿った一次元の積分を
線積分と呼ぶ。
スカラー場の線積分
スカラー場の線積分に簡単に触れておこう。
詳しくはこちら。
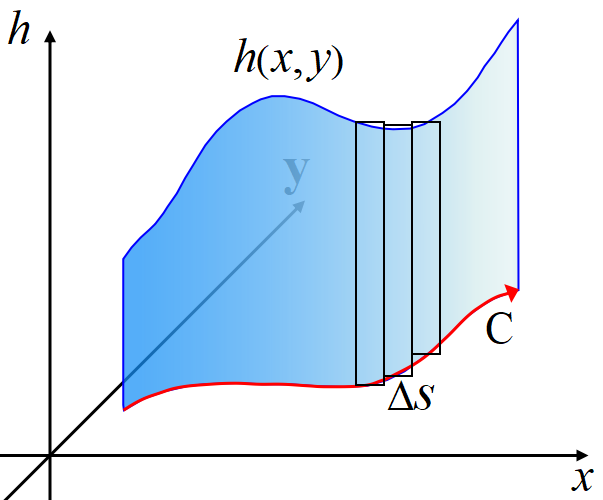
\((x,y)~\)平面上の各点で\(~h(x,y)~\)が与えられているとする。\((x,y)~\)平面上の曲線\(~\rm C~\)上に微小長さ\(~\varDelta s~\)を取る。
\[\sum h(x,y)\varDelta s\to \int_Ch(x,y)ds \]
を\(~\rm C~\)に沿った線積分と呼ぶ。図の青色カーテンの面積であり, 高校数学の直線上の積分の自然な拡張である。
が, 対応する物理量が思いつかない。ネットで調べると, \(\rm C~\)を墨汁で書いた線, \(h(x,y)~\)を墨汁の濃淡とすると, 線積分値は, 墨汁の総量を表す, とあった。相当苦労して考えた形跡がうかがえる。
ベクトル場の線積分 対応する物理量は非常に多い。ポテンシャル概念に直結。
空間内の一点\(~\bm{r}~\)に対し, ベクトル\(~\Vec A(\bm{r})~\)が一つ定まるとき, \(\Vec A(\bm{r})~\)をベクトル場と呼ぶ。例えば
\[\Vec A(\bm{r})=(A_1,A_2,A_3) \]
は, 始点が\(~(x,y,z)~\), 成分が\(~(A_1,A_2,A_3)~\)のベクトルを表すベクトル場である。\(d\bm{r}=(dx,dy,dz)~\)とすれば,
\[\int_C\Vec A\cdot d\bm{r}=\int_C A_1dx + A_2dy+A_3dz \]
\[\int_C\Vec Ads=\bm{e}_1\int_CA_1ds+\bm{e}_2\int_CA_2ds+\bm{e}_3\int_CA_3ds \]
\[\int_C\Vec A\x d\bm{r}=\bm{e}_1\int_C(A_2dx_3-A_3dx_2)+\bm{e}_2\int_C(A_3dx_1-A_1dx_3)+\bm{e}_3\int_C(A_1dx_2-A_2dx_1) \]
は全てベクトル場の線積分である。
物理では, ポテンシャルという概念との相性の良さから, 殆どは一番上の内積形をベクトル場の線積分と言う。
例えば, \(\Vec A(\bm{r})=(P(x,y),Q(x,y)\)), \(d\bm{r}=(dx,dy)~\)とすると,
\[d'W=\Vec A(\bm{r})\cdot d\bm{r}=P(x,y)dx+Q(x,y)dy\tag{3} \]
は\(~\Vec A(\bm{r})~\)が物体に働く力の場合, 物体が\(~\bm{r}~\)から\(~\bm{r}+d\bm{r}~\)へと微小移動したときに, 力\(~\Vec A(\bm{r})~\)が物体に為した仕事である。
(3)式右辺を
1次微分形式(または1形式, 厳密には外積(ウェッジ積)を用いて定義される.)と呼ぶ。
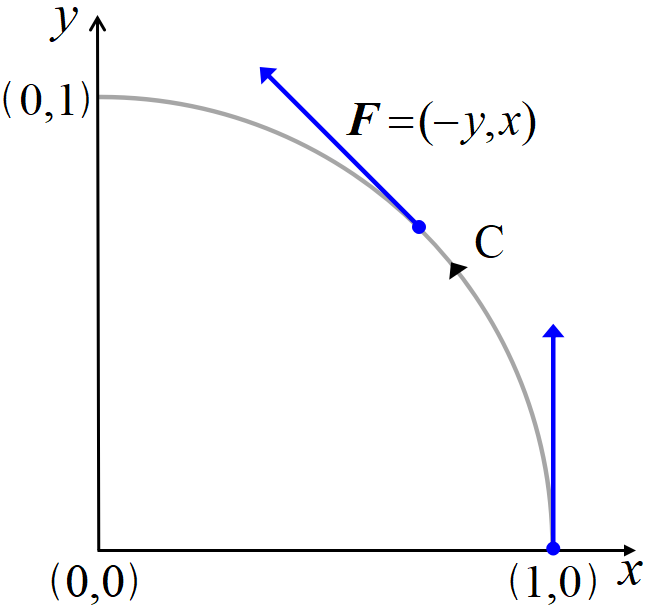
実際に計算して見よう。図は有名な\(~\Vec F=(-y,x)~\)の
回転ベクトル場である。ベクトルの大きさは見やすい様に\(~1/2~\)にしてある。
\((1,0)~\)から\(~(0,1)~\)までの線積分は, \(\Vec F(\bm{r})\cdot d\bm{r}=(-y)dx+xdy\), および\(~(x,y)=(cost,sint)~\) だから
\[\int_C(-y)dx+xdy=\int_{0}^{\pi/2}dt \left[(-y)\frac{dx}{dt}+x\frac{dy}{dt}\right]
=\int_{0}^{\pi/2}dt[-sint\x (-sint)+cost\x cost]=\frac{\pi}{2} \]
微小線素\(~ds=\sqrt{{dx}^2+{dy}^2}=\sqrt{1+(dy/dx)^2}\;dx~\)を用いる方法もあるが, 特別な場合を除き複雑になる。
円周に沿った力\(~\Vec F=(-y,x)~\)が, 半径\(~1~\)の円周上の物体を\(~1/4~\)周移動させると, \(~\pi/2~\)の仕事をするという訳である。
経路に依存しないベクトル場の線積分(1)
関数\(~\Vec F(\bm{r})~\)を任意に選んだ時, \(d'W~\)の線積分, つまり仕事は一般に辿る道筋に依存するが, 経路によらない場合がある。
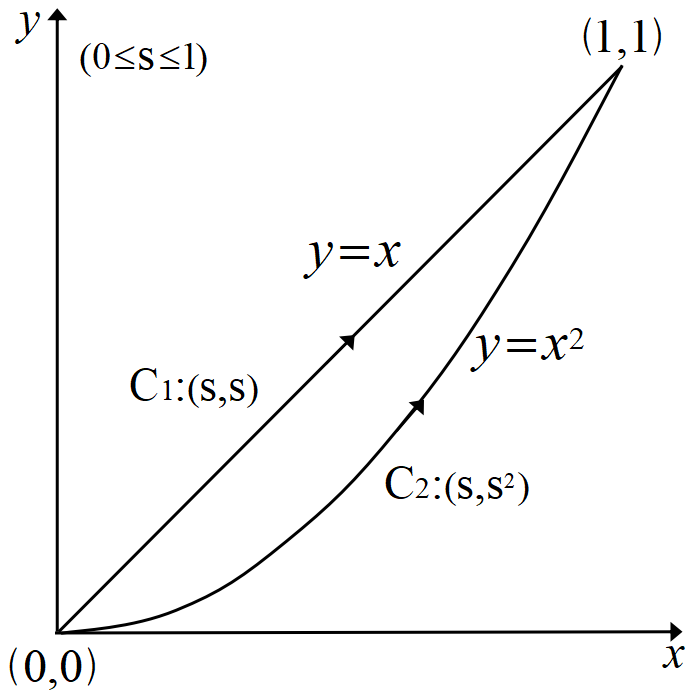
\(d'W~\)を原点\(~(0,0)~\)から点\(~(1,1)~\)へ2つの経路で線積分し, この様子を見てみよう。積分は微小線素\(~ds~\)ではなく, 媒介変数(パラメーター)で行う。
経路\(~C_1,\;C_2~\)を, パラメーター\(~s\;(0\le s\le 1)~\)を用いて, \(C_1(s,s),C_2(s,s^2)~\)とする。
例1\(~\Vec F(\bm{r})=(2y,3x)\)の場合。
(1)\(~C_1~\)に沿った線積分
経路\(~C_1(s,s)~\)における力\(~\Vec F=(2y,3x)~\)と微小変位\(~d\bm{r}=(dx,dy)~\)を\(~s~\)で表すと,
\[\Vec F=(2s,3s),\quad d\bm{r}=(ds,ds) \]
である。従って経路上を\(~s\to s+ds~\)と移動した時の微小仕事\(~d'W~\)は
\[d'W=\Vec F\cdot d\bm{r}=2sds+3sds=5sds \]
\(C_1~\)に沿っての全仕事\(~\varDelta W_1~\)は
\[\varDelta W_1=\int_{C_1}d'W=\int_{0}^{1}5sds=\frac{5}{2} \tag{4} \]
と求まる。
(2)\(~C_2~\)に沿った線積分
経路\(~C_2(s,s^2)~\)における力\(~\Vec F=(2y,3x)~\)と微小変位\(~d\bm{r}=(dx,dy)~\)を\(~s~\)で表すと,
\[\Vec F=(2s^2,3s),\quad d\bm{r}=(ds,2sds) \]
である。従って経路上を\(~s\to s+ds~\)と移動した時の微小仕事\(~d'W~\)は
\[d'W=\Vec F\cdot d\bm{r}=2s^2ds+6s^2ds=8s^2ds \]
\(C_2~\)に沿っての全仕事\(~\varDelta W_2~\)は
\[\varDelta W_2=\int_{C_2}d'W=\int_{0}^{1}8s^2ds=\frac{8}{3}\tag{5} \]
と求まる。この場合(4)と(5)は一致しない。
改めて言葉で整理すると, 力\(~\Vec F(\bm{r})=(2y,3x)~\)のベクトル場に於ける仕事は経路に依って異なる。すなわち力\(~\Vec F(\bm{r})=(2y,3x)~\)は保存力ではない。
例2\(~\Vec F(\bm{r})=(2xy^3,3x^2y^2)\)の場合。
(1)\(~C_1~\)に沿った線積分
経路\(~C_1(s,s)~\)における力\(~\Vec F=(2xy^3,3x^2y^2)~\)と微小変位\(~d\bm{r}=(dx,dy)~\)を\(~s~\)で表すと,
\[\Vec F=(2s^4,3s^4),\quad d\bm{r}=(ds,ds) \]
である。従って経路上を\(~s\to s+ds~\)と移動した時の微小仕事\(~d'W~\)は
\[d'W=\Vec F\cdot d\bm{r}=2s^4ds+3s^4ds=5s^4ds \]
\(C_1~\)に沿っての全仕事\(~\varDelta W_1~\)は
\[\varDelta W_1=\int_{C_1}d'W=\int_{0}^{1}5s^4ds=1\tag{6} \]
と求まる。
(2)\(~C_2~\)に沿った線積分
経路\(~C_2(s,s^2)~\)における力\(~\Vec F=(2xy^3,3x^2y^2)~\)と微小変位\(~d\bm{r}=(dx,dy)~\)を\(~s~\)で表すと,
\[\Vec F=(2s^7,3s^6),\quad d\bm{r}=(ds,2sds) \]
である。従って経路上を\(~s\to s+ds~\)と移動した時の微小仕事\(~d'W~\)は
\[d'W=\Vec F\cdot d\bm{r}=2s^7ds+6s^7ds=8s^7ds \]
\(C_2~\)に沿っての全仕事\(~\varDelta W_2~\)は
\[\varDelta W_2=\int_{C_2}d'W=\int_{0}^{1}8s^7ds=1\tag{7} \]
と求まる。今度は(6)と(7)が一致した。
これも言葉で整理すると, 力\(~\Vec F=(2xy^3,3x^2y^2)~\)のベクトル場に於ける仕事は経路に依存しない。すなわち力\(~\Vec F=(2xy^3,3x^2y^2)~\)は保存力である。
経路に依存しないベクトル場の線積分(2) 当たり前なのだろうが, 上手くできている。
(4)~(7)式では\(~s:0\to 1~\)まで積分してしまったので結果は分かるが, 途中の経過\(~0\le (x,y)\le 1~\)が分からない。
\(W(\bm{r})~\)はどのような形をしているのだろうか?\(~\Vec F=(2xy^3,3x^2y^2)~\)で求めて見よう。
(経路に依らないので)積分経路は任意であるが, 計算しやすい直線\(~C_1~\)で行う。\(~C_1~\)上の点\(~\bm{r}(x,y)~\)は,
\[\bm{r}=(xs,ys),\quad 0\le s\le 1 \]
と表せる。この点における微小仕事, \(d'W=\Vec F\cdot d\bm{r}~\)は,
\[\Vec F(\bm{r})=(2xy^3s^4,3x^2y^2s^4),\quad d\bm{r}=(xds,yds) \]
より,
\[d'W=\Vec F(\bm{r})\cdot d\bm{r}=2x^2y^3s^4ds+3x^2y^3s^4ds=5x^2y^3s^4ds \]
これを 0 から 1 まで積分する。(4)~(7)式の積分は\(~x~\)も\(~y~\)も 0~1 であるが, 今回の積分は 0~\(~x\), 0~\(~y\)である。関数\(W(x,y)~\)は
\[W(x,y)=\int_{0}^{x}\int_{0}^{y}dW=5x^2y^3\int_{0}^{1}s^4ds=x^2y^3\tag{8} \]
となる。ここで勾配\(~\nabla W(x,y)~\)を求めて見よう。
\[\nabla W(x,y)=\left(\dd{W}{x},\dd{W}{y}\right)=(2xy^3,3x^2y^2) \]
すなわち,
\[\Vec F(\bm{r})=(-)\nabla W(\bm{r}) \]
となっている。つまり\(~\Vec F(\bm{r})~\)は, 関数\(~\Vec W(\bm{r})~\)の勾配に他ならない。
(ー)は物理固有の表現で, ポテンシャルを微分したとき, 微分が表す力が正しい方向を示すためである。数学的には不要である。
同様の計算を\(~\Vec F(\bm{r})=(2y,3x)~\)について行うと,
\[\Vec F(\bm{r})=(2ys,3xs),\quad d\bm{r}=(xds,yds) \]
より,
\[d'W=\Vec F(\bm{r})\cdot d\bm{r}=2xyds+3xyds=5xyds \]
これを 0 から 1 まで積分する。(4)~(7)式の積分は\(~x~\)も\(~y~\)も 0~1 であるが, 今回の積分は 0~\(~x\), 0~\(~y\)である。関数\(W(x,y)~\)は
\[W(x,y)=\int_{0}^{x}\int_{0}^{y}dW=5xy\int_{0}^{1}sds=\frac{5}{2}xy \]
となる。ここで勾配\(~\nabla W(x,y)~\)を求めると,
\[\nabla W(x,y)=\left(\dd{W}{x},\dd{W}{y}\right)=\left(\frac{5}{2}y,\frac{5}{2}x\right) \]
となり, 今度は
\[\Vec F(\bm{r})\neq (-)\nabla W(\bm{r}) \]
であり, \(\Vec F(\bm{r})=(2y,3x)~\)は\(~W(x,y)=5/2\;xy~\)の勾配とはならない。
ところで, 保存ベクトル場\(~\Vec F(\bm{r})=(2xy^3,3x^2y^2)~\)と, 非保存ベクトル場\(~\Vec F(\bm{r})=(2y,3x)~\)のそれぞれと, 微小ベクトル\(~d\bm{r}=(dx,dy)~\)との内積,
\[\phi=2xy^3dx+3x^2y^2dy,\quad\psi=2ydx+3xdy \]
を見ると, 前者は後者に\(~M(x,y)=xy^2~\)を乗じたもので, この\(~M(x,y)~\)を\(~\psi~\)の
積分因子と呼ぶのであった。
そして積分因子を乗じた完全微分方程式
\[2xy^3dx+3x^2y^2dy=0 \]
の解が
\[\Phi(x,y)=x^2y^3=C \]
であった。この\(~\Phi(x,y)=x^2y^3~\)は(8)式\(~W(x,y)~\)と一致している。