楽しく学ぶ…熱力学
エントロピー(1) クラウジウスの不等式
エネルギーと並ぶ, しかし異なる側面を照らす根本原理。
1865年, クラウジウスは, 「エントロピー」という語句を考案し, チューリヒ哲学会で高々と宣言した。
(1)宇宙のエネルギーの量は一定である。
(2)宇宙のエントロピーは最大値に向かって増えて行く。
エントロピー登場 精緻なカルノーサイクルと純粋に数学的な知見から得られた大発見。
ケルビンの絶対温度導出の過程から
\[\frac{Q_H}{T_H}=\frac{Q_L}{T_L} \tag{1}\]
が得られた。高温熱源に関連する
「何か」\(\displaystyle \frac{Q_H}{T_H}~\)と低温熱源に関連する
「何か」\(\displaystyle \frac{Q_L}{T_L}~\)が等しいということである。
クラウジウスは当初, 単位温度当たりに正規化した熱量, \(Q_H/T_H,\;Q_L/T_L~\)を「換算熱」と呼んでいた。
ところで熱量\(~Q_H,\;Q_L~\)であるが, \(Q_H~\)を取り込んで\(~Q_L~\)を捨てるという風に, 両方共, 正の値として考察して来た。
そこで, 今後は入ってくる熱量は正, 出て行く熱量は負と約束し,
(1) 系が熱\(~Q \gt 0~\)を受け取るときは\(~q=Q\gt 0\)
(2) 系が熱\(~Q \gt 0~\)を放出するときは\(~q=-Q\lt 0~\)(負の熱量を受け取る)
とし, 大文字の\(~Q~\)は原則, 値は正として, 象徴的な説明が必要な場で用いることとしよう。
\(H\to 1,\;L\to 2~\)とすると(1)式は
\[\begin{align}
&\frac{q_1}{T_1}=-\frac{q_2}{T_2}\quad(q_1\gt 0,\;q_2\lt 0) \\
&\frac{q_1}{T_1}+\frac{q_2}{T_2}=0 \tag{2}
\end{align} \]
と表せる。
さてここまでは一つの高温熱源\(~T_1(T_H)~\),一つの低温熱源\(~T_2(T_L)~\), 一つのカルノー機関\(~C_1(T_1,\;T_2)~\)を考えてきた。
ここで
並列に動作する複数のカルノー機関\(~C_1(T_1,\;T_2)~\), \(~C_2(T_3,\;T_4)~\)‥‥\(~C_m(T_{n-1},\;T_{n})~\)を考える。
夫々の機関で(2)式が成り立っているはずだから,
\[\frac{q_1}{T_1}+\frac{q_2}{T_2}+\frac{q_3}{T_3}+\frac{q_4}{T_4}+
\dots+\frac{q_{n-1}}{T_{n-1}}+\frac{q_{n}}{T_{n}}=0 \tag{3} \]
ここまでくれば\(~q,\;T~\)をいちいち高温部, 低温部と区別する必要もないだろう。
\(i~\)番目の熱源の温度を\(~T_i~\)とし, そこからもらう熱を\(~q_i~\)とする。捨てる場合には負の値となる。すると, (3)式を
\[\sum_{i}\frac{q_i}{T_i}=0 \tag{4} \]
として良いだろう。(4)式の等号を不等号\(~(\le)~\)にしたものがクラウジウスの不等式である。
クラウジウスは, \(\varDelta Q_i/T_i~\)を特別な量と考え,
\[\varDelta S=\frac{\varDelta Q}{T} \]
として, これを「エントロピー」と名付けた。\(dS~\)ではなく, \(\varDelta~\)を用いたのは習慣上であって深い意味はない。
エントロピーの厳密な定義は「積分形による表現」で行う。それまでは熱量\(~Q~\)を絶対温度\(~T~\)で割った量, くらいで妥協しよう。
クラウジウスは当初「換算熱」と呼んでいたが, 重要性に気付き新たに命名した。ギリシャ語で\(en~\)は「中へ」を, \(trope~\)「変化,変換」を意味する。
原子の実在性を全く前提とせず, 啓蒙書などで良く使われる「デタラメさの尺度」と言った意味は全く無かった。
\(S~\)はクラウジウスが選んだ文字である。サディ(\(~Sadi~\))・カルノーに敬意を表して選んだらしい。
クラウジウスの不等式 カルノーサイクルに秘められたエントロピーの出発点。
クラウジウスの不等式 (1) 簡単な説明だが, もっとも本質的。
(2)式は準静的過程で成り立ち, この状態の達成には無限の時間を要する。カルノー機関を動作させるためには, 高温熱源は\(~T_1~\)よりわずかに高く\(~T_1+\delta T_1~\), 低温熱源は\(~T_2~\)よりわずかに低く\(~T_2-\delta T_2~\)でなければならない。\(q_2~\)が負であることを考えれば(2)式は
\[\frac{q_1}{T_1}+\frac{q_2}{T_2}\le 0 \tag{5} \]
となる。これがクラウジウスの不等式である。等号は熱機関が可逆な場合である。
言葉で言えば低温熱源へ捨てたエントロピー\(~(-q_2/T_2)~\)は, 高温熱源から得たエントロピー\(~(q_1/T_1)~\)より大きい, ということである。
ここの可逆, 不可逆は極めて重要で, 温度が\(~T\neq T_i~\), すなわち不可逆過程の場合は, エントロピー\(~(q_i/T_i)~\)は
積分によって算出できないことが後になって分かるであろう。
クラウジウスの不等式 (2) この説明も多い。循環論法ではないか? いつも気になる。
熱機関の効率\(~\eta~\)は投入された熱\(~Q_H~\)に対する仕事\(~W=Q_H-Q_L~\)の割合で
\[\eta=\frac{Q_H-Q_L}{Q_H}=\frac{q_1+q_2}{q_1}=1+\frac{q_2}{q_1}\tag{6} \]
と表せる。可逆機関の場合, 効率\(~\eta_C~\)は高温熱源と低温熱源の温度で表せる。
\[\eta_C=1-\frac{T_2}{T_1}\tag{7} \]
可逆機関の効率が最大であるから, (6), (7) に\(~\eta \leq \eta_C ~\)を適用して,
\[1+\frac{q_2}{q_1}\leq 1-\frac{T_2}{T_1}\]
両辺に\(~\displaystyle \frac{q_1}{T_2}~\)を掛けて,
\[\frac{q_1}{T_1}+\frac{q_2}{T_2}\leq 0 \]
同じ結果が得られた。等号は\(~\eta=\eta_C~\), すなわち熱機関が可逆な場合である。
クラウジウスの不等式 (3) 正統的な説明だが1回読んでも解らない。
ともかく分かり難い。正確を期すために同じ語句を何度も繰り返すが, しばらく我慢!
今までは熱源は高温\(~T_H~\)と低温\(~T_L~\)の2種類のみであったが, これを複数の熱源\(~T_i~\)との間で動作する多温度サイクル\(~S~\)に一般化する。
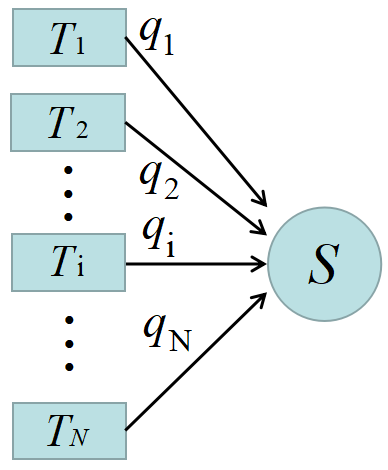
任意の多温度サイクル\(~S~\)は, 温度\(~T_1,\;T_2,\dots,T_N~\)の熱源から熱\(~q_1,\;q_2,\dots,q_N~\)を受け取り, 外界と仕事のやりとりをする。
矢印\(~(\to)~\)は全て\(~S~\)に向かっているが, この中には熱源へ熱\(~q_i~\)を放出する(負の熱量を受け取る)場合もある。
例えば\(~q_2~\)が負の場合, 高温熱源\(~T_1~\)から熱量\(~q_1~\)を受け取り, 低温熱源\(~T_2~\)へ熱量\(~|q_2|~\)を捨てるサイクルもあり得るということである。
また多温度サイクル\(~S~\)は一般のものを考えているので,
可逆であっても不可逆であってもよい。
これに対し, 次に述べるサイクル\(~C_i~\)は,
完全に可逆なサイクルである。ここのところがはっきりしない解説が多い。
当然\(~S~\)は仕事をしたりされたりするわけであるが, ここでは省略してある。
この多温度サイクル\(~S~\)に, \(N~\)個の
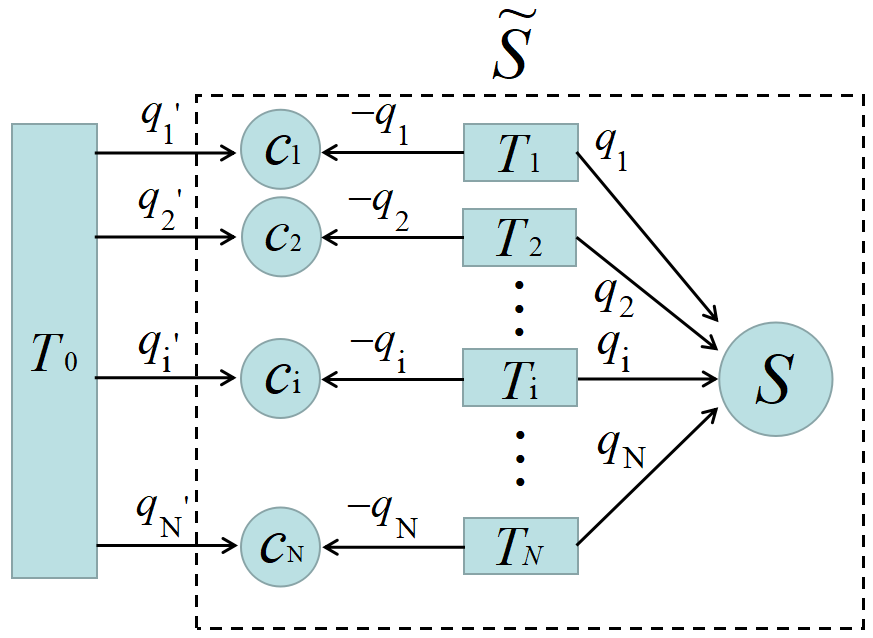
可逆カルノーサイクル\(~C_1,\;C_2,\;\dots C_N~\)を組み合わせて動作させる。\(~C_i~\)は新たな共通の熱源\(~T_0~\)と, 元々あった熱源\(~T_i~\)の間で熱のやり取りをするものとする。矢印は全て\(~N~\)個のサイクル\(~C_1\sim C_N~\)に向かっていることに注意しよう。
\(C_i~\)は\(~T_0~\)から\(~q'_i~\)の熱を受け取り, \(T_i~\)からは\(-q_i~\)の熱を受け取るものとする。\(-q_i~\)だから負というわけではない。
例えば\(~q_2\lt 0~\)ならば, \(|q_2|~\)の熱がサイクル\(~S~\)から\(~T_2~\)へ流れ出し(この場合\(~T_2~\)は\(~S~\)の低温熱源), \(-q_2(\gt 0)~\)の熱がサイクル\(~c_2~\)へ流れ込む(この場合\(~T_2~\)は\(~c_2~\)の高温熱源)。
\(~C_i~\)は可逆サイクルであるから, 個々のカルノーサイクル\(~C_i~\)で(2)式と同様に,
\[\frac{q'_i}{T_0}+\frac{(-q_i)}{T_i}=\frac{q'_i}{T_0}-\frac{q_i}{T_i}=0 \]
が成り立っている。従って\(~C_1\sim C_N~\)を全てを加えた,
\[\sum_{i=1}^{N}\frac{q_i'}{T_0}-\sum_{i=1}^{N}\frac{q_i}{T_i}=\frac{1}{T_0}\sum_{i=1}^{N}q_i'-\sum_{i=1}^{N}\frac{q_i}{T_i}=0\tag{8} \]
が成り立つ。
熱源\(~T_i~\)に注目すると, \(S~\)へ\(~q_i~\)を放出し, \(C_i~\)へ\(~-q_i~\)を放出しているので正味の熱の収支は0で, 考えなくとも良い。
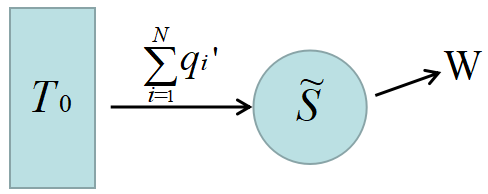
そこで, 多温度サイクル\(~S~\)と\(~N~\)個のカルノーサイクル\(~C_1,\;C_2,\;\dots C_N~\)を一つにまとめて\(\tilde{S}~\)としよう。
\(\tilde{S}~\)は一つの熱源\(~T_0~\)から熱量\(~\displaystyle \sum_{i=1}^{N} q'_i~\)を受け取って(上記矢印の中には熱源\(~T_0~\)へ熱を放出する過程も含まれる.)作用するサイクルと考えられる。
仕事を外向きに\(~W~\)と書くことにすると, 等温\(~\rm T_0~\)だから内部エネルギーは変化せず, 熱力学第一法則(可逆でも不可逆でも成り立つ.)から
\[W=\sum_{i=1}^{N}q'_i\tag{9} \]
である。
ケルビンの原理は「一つの熱源とのみ熱のやり取りをして正の仕事を生み出すことは出来ない」とも表現される。
ケルビンの原理図を再掲しよう。
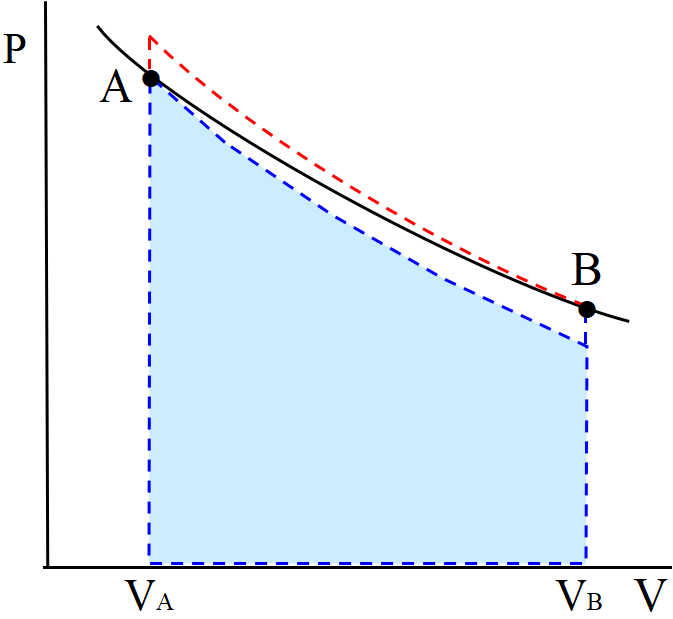
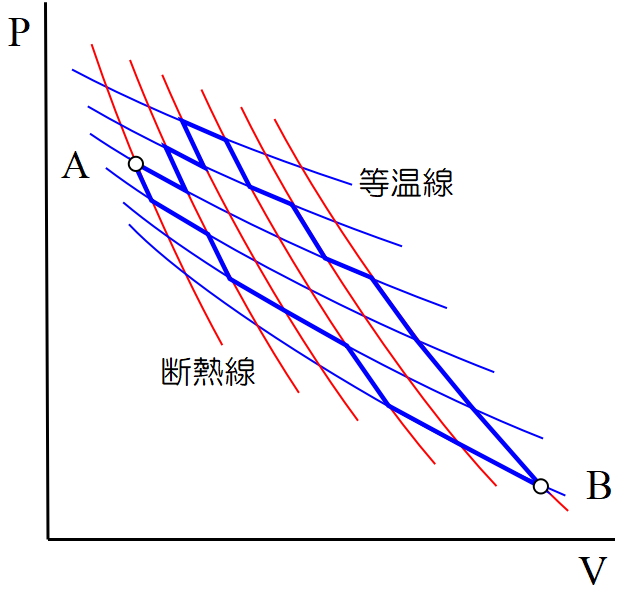
熱源が\(~A\sim B~\)の等温線(温度\(~T_0~\))1つのみで, 図の\(~A\to B\to A~\)として正の仕事は不可能であるのは明らかだろう。よって(9)式の仕事\(~W~\)は,
\[W=\sum_{i=1}^{N}q'_i\le 0\tag{10} \]
である。等号は\(~A\to B\to A~\)が可逆過程の場合に成り立つ。(8)式を適用するために(10)式を\(T_0(\gt 0)~\)で割って
\[\frac{1}{T_0}\sum_{i=1}^{N}q_i'\le 0\tag{11} \]
可逆カルノーサイクル\(~C_1\sim C_N~\)で成り立っている(8)式
\[\frac{1}{T_0}\sum_{i=1}^{N}q_i'-\sum_{i=1}^{N}\frac{q_i}{T_i}=0 \]
と, (11)式から
\[\sum_{i=1}^{N}\frac{q_i}{T_i}\le 0\tag{12} \]
を得る。
クラウジウスの不等式である。等号は\(\tilde{S}~\)が可逆, すなわち\(~S~\)が可逆サイクルの場合に成り立つ。
また,
(10)式ケルビンの原理と(12)式クラウジウスの不等式は同値である, のも理解される。
(不可逆過程も含む)任意のサイクル\(~S~\)が熱源\(~T_i~\)とやり取りする熱量\(~q_i~\)を熱源の温度で割った\(~q_i/T_i~\)を全て加えると負になる。つまりクラウジウスの不等式は, \(~q_i/T_i~\)をエントロピーと呼ぶと, 熱源からもらうエントロピーより, 熱源へ捨てるエントロピーのほうが大きい事を示している。
エントロピーは, そのプロセスが可逆変化(準静的過程)かどうかに強く依存する。一方, 熱力学第一法則(エネルギー保存則)は可逆, 不可逆に関係なく成り立つ。この辺りもエントロピーが分かり難い原因だろうか?もっともエネルギー保存則も紆余曲折を経て生まれたのであるが!
改めて書くと, 複数の熱源\(~T_1,\;T_2,\dots~\)と熱のやり取りをしている適当なサイクル\(~S~\)において, \(S~\)が可逆サイクルならば
\[\sum_{i}\frac{q_i}{T_i}=0 \tag{13} \]
となり, \(S~\)が不可逆サイクルならば
\[\sum_{i}\frac{q_i}{T_i}\lt 0\tag{14} \]
となる。これはサイクル\(S~\)が熱源と
エントロピー\(~q/T~\)のやり取りをしていると見ることが出来る。
少し説明を加えると, エントロピーを単に, \(~q~\)を\(~T~\)で割ったものでは無く, 新しい状態量として考えようということである。
ギブスの自由エネルギーでは, エントロピー\(~q/T~\)は, 熱\(~q~\)より遥かに重要な
示量性状態量である。ギブスは内部エネルギー\(~U~\)の変数を\(~U(S,V)~\)とすべきと指摘している。
熱力学は, 階層的に分かれているのではなく, 渾然一体となっている。一度高見に登って全体を見渡さないと, なかなか理解できない。
積分へのステップ
熱源の数\(~\rm N~\)を十分大きくすれば, 熱源とやり取りする全ての\(~q_i~\)を十分小さく出来る。
サイクル\(S~\)が各熱源とやり取りする微小な熱を\(~\varDelta'q_i~\)(\(~\varDelta'q_i\gt 0~\)は吸熱,\(~\varDelta'q_i\lt 0~\)は放熱)とすると, (13)と(14)をまとめて:
\[\sum_{i=1}^{N}\frac{\varDelta'q_i}{T_i}\le 0\tag{15} \]
を得る。熱源の温度が変化する場合も, 僅かに温度が異なる多数の熱源を用意すれば, 近似的に(15)式の様に書ける。
熱量\(~q~\)は状態量ではない事を明示的に示すために, (15)式で\(~\varDelta '~\)(ダッシュ)を付けた。
積分形による表現 数学的背景は
積分因子参照。
前節では多数の, 並列に動作するカルノーサイクルを考えたが, 微小なカルノーサイクルを寄せ集めても, 同様の式が成り立ちそうである。
例えば\(~\rm A\to B\to A~\)というサイクルは, 図のような, 多数の等温線と断熱線に沿って移れば実現できる。個々の小さな四角形がカルノーサイクルを表していることは明らかであろう。
隣り合うカルノーサイクルで, 共通の等温曲線, 断熱曲線で熱の収支が打ち消し合うので, 一番外側のカルノーサイクルだけが残る。
さて, わずかに温度の異なる無限に多くの熱源と無数のカルノー機関を考えれば, \(~\sum~\)は積分で置き換えられ,
\[\oint_C \frac{d'Q}{T}=0\tag{16} \]
となるだろう。\(d'Q~\)は\(~Q~\)が状態量でないことを忘れないために明示的に記した。大文字の\(~Q~\)は具体的な計算というより, 象徴的な意味で用いた。
可逆カルノー機関1サイクルでは元の状態に戻る。無数に分割したカルノーサイクル図からもその様に思える。そうすれば(16)式のエントロピーは状態量であるように思える。果たして状態量ではない\(~d'Q~\)を, 温度\(~T~\)で割った\(~d'Q/T~\)を積分して良いものだろうか?
\(d'Q/T~\)が積分可能かと言う議論はあるが, 今は妥協して積分の形を求めて見よう。
互いに共通の断熱曲線, 等温曲線を介して隣接する\(~n~\)個(図では15個)のカルノーサイクルを考えると, 一番外側の経路(青太線)を除いた内部では, 隣接するカルノーサイクル通しで打ち消しあうため, 青色の周辺部分だけが, 熱の出入りを計算するための, 正味の経路ということになる。そして, \(~n~\)個のカルノーサイクルの熱の出入りについては断熱線も含めて,
\[\frac{q_1}{T_1}+\cdots +\frac{q_m}{T_m}=0 \tag{17} \]
が成り立っている(図では\(~m=20~\))。ただし断熱線では\(~q_i=0~\)である。
ここで, 分割されたカルノーサイクルのサイズを無限小とする極限操作を行うと, (16)式は, 閉曲線\(~\rm C~\)(青太線)上の線積分を用いて,
\[\oint \frac{d'q_{rev}}{T}=0 \]
と書けるであろう。右辺が 0 となるのは準静的過程(可逆過程)の時のみであることを忘れてはならない。
\(rev~\)は可逆過程\(~(reversible\; process)~\)の略である。
微小なカルノーサイクルの組み合わせによって, 閉曲線\(~\rm C~\)を任意の形状にできることも明らかであろう。
上式を
\[\oint \frac{d'q}{T}\le 0 \]
として, これをクラウジウスの不等式と呼ぶ場合も多い。不等号は, 熱\(~d'q~\)が不可逆過程で移動した場合である。
以上を要約すると「任意の閉じた経路で\(~d'q/T~\)を積分すると, 負または\(~0~\)となる」ことを示している。
\(0~\)は可逆過程, 負は不可逆過程である。
ベクトル解析の知見によると, このような状況を満たす領域では, いわゆるポテンシャル関数が存在し, 任意の2点\(~\rm A~\)から\(~\rm B~\)への\(~d'q/T~\)の線積分は始点と終点だけで決定される。その “ポテンシャル関数”を\(~S~\)とすれば, 点\(~\rm A~\)から\(~\rm B~\)までの積分は,
\[\int_{A}^{B} \frac{d'q_{rev}}{T}=S(B)-S(A) \tag{18} \]
と表すことが可能である。ここで, \(S(B),\;S(A)~\)はそれぞれ, 点\(~\rm B~\), または点\(~\rm A~\)だけで定まる量なので
状態量である。
この状態量\(~S~\)がエントロピーの厳密な定義である。\(~d'q/T~\)の代わりに
\[\frac{d'q_{rev}}{T}=dS \]
も良く用いられる。\(d'q_{rev}~\)は可逆過程で発生(吸収)する熱量である。可逆過程を強調するため, \(~(rev)~\)を記した。
少々くどいが, 誤解し易いところなので繰り返し述べる。
(18)式で定義した, 状態量を表すポテンシャル関数エントロピー(又はエントロピーの変化)\(S~\)は可逆過程でのみ意味を持つ。不可逆過程で積分を行ってもその結果は意味を持たず, ポテンシャル関数で無い事は言うまでもない。
周回積分\(~0~\)とポテンシャル関数
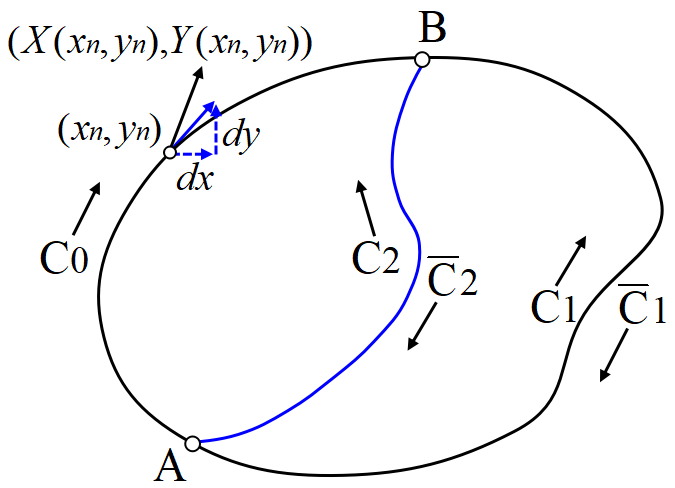
デカルト座標に, ある方向を持った曲線\(~s~\)が与えられているとする。この曲線上の点を\(~(x,y)~\)とし, 各点に連続な関数 \(~X(x,y)~\), \(Y(x,y)~\)が定義されているとする。
曲線\(~s~\)上の微少部分\(~ds~\)の成分を\(~(dx,dy)~\)とし, \(X(x,y)dx+Y(x,y)dy~\)を計算する。\((X(x,y),Y(x,y))~\)がベクトル場ならば, ベクトルの内積であり, スカラー場ならば, ただの計算である。
つまり\(~(X(x,y),Y(x,y))~\)はベクトル場でもスカラー場でも良い。このとき,
\[\int X(x,y)dx+Y(x,y)dy \]
を曲線\(~s~\)上の線積分と呼ぶ。
線積分のさらに詳しい説明はこちら。
\(~A\to B\to A~\)の任意のループ\(~C~\)に沿った, 関数\(~X(x,y),Y(x,y)~\)の周回線積分の値が\(~0~\)であるとする。
\(X(x,y)dx+Y(x,y)dy~\)を\(~Z(r)dr~\)と書くと, \(C=C_0+\overline C_1~\)のとき,
\[\oint_{C}Z(r)dr=\int_{C_0}Z(r)dr+\int_{\overline C_1}Z(r)dr=0 \]
\(C=C_0+\overline C_2~\)のとき
\[\oint_{C}Z(r)dr=\int_{C_0}Z(r)dr+\int_{\overline C_2}Z(r)dr=0 \]
2つの式を比べて,
\[\int_{\overline C_1}Z(r)dr=\int_{\overline C_2}Z(r)dr \]
積分の向きを変えれば,
\[\int_{C_1}Z(r)dr=\int_{C_2}Z(r)dr\tag{19} \]
を得る。\(C_1,\;C_2~\)は任意であるから, (19)式は, \(A~\)から\(~B~\)への線積分は経路によらず, 始点\(~A~\)と終点\(~B~\)だけで決まることを意味している。したがって, 積分値は位置\(~A,B~\)だけを変数とする適当な関数\(~G(A,B)~\)で表せる。
さらに, 積分経路を\(~A\to B~\)から\(~B\to A~\)にすれば, 積分値の符号が逆になることから, \(G(A,B)=-G(B,A)~\)を満たす必要がある。これは, ある関数\(~F~\)を用いて, \(G(A,B)=F(B)-F(A)~\)と書き換えられることを意味する。つまり,
\[\int_{A}^{B}Z(r)dr=F(B)-F(A) \]
と書ける。積分の始点を\(~F(A)=0~\)とし, \(B~\)を一般化して\(~r~\)と書いて,
\[F(r)=\int_{A}^{r}Z(r)dr \]
を, ポテンシャル関数と呼ぶ。(変数を\(x~\)とすると, 1変数と誤解される恐れがあるので, \(~r~\)とした.)
周回積分\(~0~\)は関数\(~F(r)~\)がポテンシャル関数であるための十分条件である。