楽しく学ぶ…熱力学
理想気体のカルノーサイクル
一度は具体的に計算してみよう。
理想気体のカルノーサイクル 教科書の図とは随分違う。実際に計算しているのだろうか?
カルノーサイクル動作原理 現実の\(~p-V~\)図はこんな形。
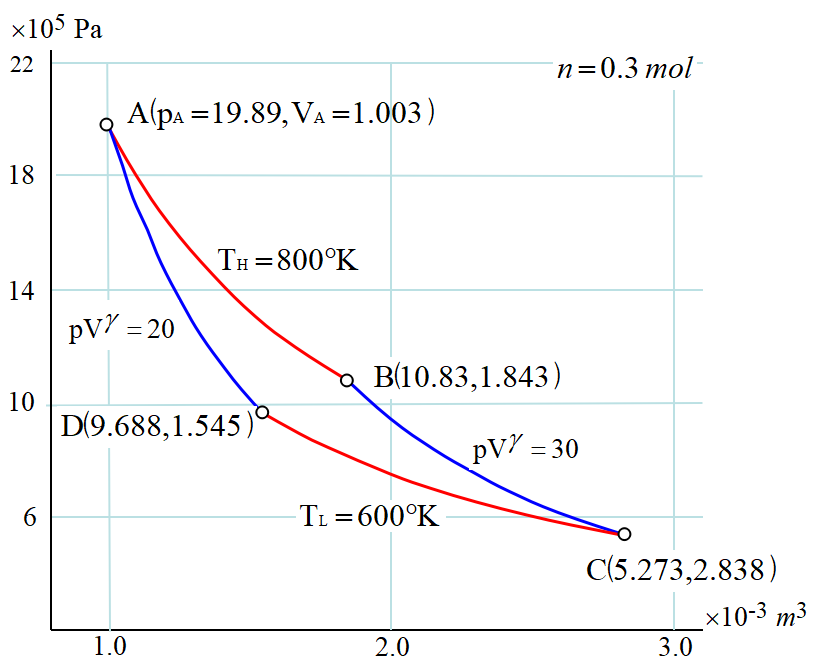
理想気体でカルノーサイクルの計算をやって見よう。複数の等温線と断熱線から選ぶわけだが, 見やすい組み合わせを選んでも図のようなものになってしまう。
因みに図の場合のエネルギー効率は25%である。もっと効率の高いものを探すと, \(B\to C~\)の断熱膨張がずっと長くなってバランスが悪くなる。
カルノーサイクルで見たように, 次の状態変化をたどる。
\(A\to B\):等温膨張。熱機関が外界に対して仕事\(~W_{AB}~\)をする部分である。高温熱源から\(~Q_H~\)を受け取り, 外界に対して仕事をする。
\[\begin{align}
W_{AB}&=\int_{A}^{B}pdV=\int_{A}^{B}\frac{nRT_H}{V}dV\\
&=nRT_H[logV]_{V_A}^{V_B} \\
&=nRT_Hlog\frac{V_B}{V_A} \tag{1}
\end{align}\]
である。この仕事は等温過程における最大仕事\(~W_{max}~\)である。
等温可逆過程の図から容易に想像できるが, 簡単に証明しておこう。
\(A\to B~\)は準静的過程であるから当然可逆過程でもある。ケルビンの原理から
\[W_{cyc}\le 0 \]
\(W_{cyc}~\)は\(~A\to B\to A~\)の1サイクルの間に, 系が外界に行う仕事である。
もし正の仕事をすることがあれば, その熱機関は温度一定の環境下で, 自分自身は変化せず次々と外界に仕事をし続ける。
すなわち
第二種の永久機関が存在することになる。(証明終わり)
この最大仕事\(~W_{max}~\)は, 後述する「ヘルムホルツの自由エネルギー」と一致する。
図の例では,
\[W_{AB}=0.3*8.314*800*log\frac{1.84}{1.00}=1.216*10^3 [J] \]
である。
理想気体の内部エネルギーは温度のみの関数だったから, 等温過程で内部エネルギーの変化はない。つまり, 高温熱源から受け取った熱\(~Q_H~\)(燃料の燃焼から得た熱)は全て\(~W_{AB}~\)へと変わる。
等温膨張が永遠に続けば効率 100% の熱機関が実現するが, そうは行かない。元の状態に戻す「サイクル動作」が必要である。
等温過程は最も基本的なプロセスであるが, \(~W_{AB}~\)は積分計算が必要なので, 高校物理, 受験問題で取り扱われる事はない。
\(B\to C\):断熱膨張。シリンダー内の空気を冷却するのが目的である。膨張で仕事をするのが目的ではないが, 実際にはかなりの仕事をする。図の場合で, 等温膨張時の 60% 位になる。ただし, \(D\to A~\)の断熱圧縮時に, 外界は系に対して全く同じ仕事をする必要があり, 熱機関の有効な出力とは言えない。
外界に為す仕事は\(~PV^{\gamma}=K\)(一定)を用いて,
\[\begin{align}
W_{BC}&=\int_{B}^{C}pdV=\int_{B}^{C}\frac{K}{V^{\gamma}}dV \\
&=K\left[\frac{V^{-\gamma +1}}{-\gamma +1}\right]_{V_B}^{V_C} \\
&=\frac{K}{-\gamma +1}(V_C^{-\gamma+1}-V_B^{-\gamma+1})\tag{2} \\
&=\frac{1}{-\gamma +1}(p_CV_C-p_BV_B) \\
&=\frac{1}{-\gamma +1}(nRT_L-nRT_H) \\
&=\frac{nR}{\gamma -1}(T_H-T_L) \\
&=\frac{3}{2}nR\varDelta T \tag{3}
\end{align} \]
となる。最後の行で\(\displaystyle~\gamma=\frac{5}{3}~\)を用いた。
高校の教科書は当然としても, 断熱過程の積分について書かれている資料は少ない。以下の説明が普通である。
熱力学第一法則\(~dU=d'Q+d'W~\)で, \(d'Q=0~\)だから, 系が為す仕事は\(~-d'W=-dU~\)。系の内部エネルギー\(~U~\)は温度のみの関数だから,
\[\begin{align}
W_{BC}&=U(T_H)-U(T_L)=C_V\varDelta T \\
&=\frac{3}{2}nR\varDelta T
\end{align}\]
積分計算の最後(3)式と同じである。当然なのだろうが, ちょっと不思議な感じがする。
因みに上図の場合(2)式を実行すると, \(\displaystyle\gamma=\frac{C_p}{C_V}=\frac{5}{3},\;pV^{\gamma}=30~\)だから,
\[\begin{align}
W_{BC}&=\frac{C}{-\gamma +1}(V_C^{-\gamma+1}-V_B^{-\gamma+1})=-45\left((2.838*10^{-3})^{-\frac{2}{3}}-(1.843*10^{-3})^{-\frac{2}{3}} \right) \\
&=-45(49.887-66.524)=748.7\;[\rm J]
\end{align} \]
となる。(3)式で計算すると,
\[W_{BC}=\frac{3}{2}*0.3*8.314*(800-600)=748.3\;[\rm J] \]
である。(2)式の積分計算は, 高校物理では文部省の方針で不可である。(3)式で逃げられるので, 入試では断熱過程は頻出する。
誤差範囲で一致してはいるが, 積分による計算は, べき乗の展開で誤差が入りやすい。実際は単位を合わせるのに相当苦労する。
\(C\to D\):等温圧縮。シリンダー内の空気を圧縮して, ピストンを元の位置に戻す。温度が上昇するので, \(Q_L~\)を低温熱源に捨てる。
外界が系に対して為す仕事は,
\[\begin{align}
W_{CD}&=\int_{C}^{D}pdV=\int_{C}^{D}\frac{nRT_L}{V}\\
&=nRT_L[logV]_{V_C}^{V_D} \\
&=nRT_Llog\frac{V_D}{V_C} \tag{4}
\end{align}\]
である。この時必要な仕事は, 等温圧縮の場合が最小である。
この最小仕事は
\[W_{CD}=0.3*8.314*600*log\frac{1.55}{2.84}=-906.2 [J] \]
である。
\(D\to A\):断熱圧縮。シリンダー内の空気を急激に圧縮して, 温度を\(~T_H~\)に上げる。
この時外界が系に為す仕事は, 断熱膨張と同様にして,
\[\begin{align}
W_{DA}&=\frac{nR}{\gamma -1}(T_L-T_H) \\
&=\frac{3}{2}nR\varDelta T
\end{align}\]
である。断熱膨張と全く同じ値であり, 断熱過程は
熱機関の効率に影響しない。
熱機関の効率 技術者の夢を砕く結果が!
「燃料の燃焼熱のうちどれだけを外部への仕事に変えたか?」が効率だろうから, 断熱過程は無視して効率\(~\eta~\)は,
\[\begin{align}
\eta&=\frac{W_{AB}}{Q_H} \\
&=\frac{Q_H-Q_L}{Q_H} \\
&=1-\frac{Q_L}{Q_H} \\
&=1-\frac{T_L}{T_H}
\end{align} \]
となる。最後の式は次の節で導かれるが, 技術者の夢を打ち砕いた結果である。どんなに工夫しても高温と低温の温度差で効率が決まってしまう。
低温側は実用的に外気温近辺に限られるから, 技術者は高温をさらに高くするしかない。現在ではガスタービンの最高温度は\(1700^{\circ} \rm C~\)に達するそうである。因みに図の場合の効率は,
\[\begin{align}
&\eta=1-\frac{Q_L}{Q_H}=1-\frac{906.2}{1216}=0.2547 \\
&\eta=1-\frac{T_L}{T_H}=1-\frac{600}{800}=0.2500
\end{align} \]
有効数字の取り方だろうが, ぴったり一致させるのは中々大変だ。
エントロピー登場 カルノーサイクルは熱機関の効率を示すだけではない!
断熱関係式 ポアッソンの関係式。等温過程では\(~pV=\)一定。断熱過程では\(~pV^{\gamma}=\)一定。
熱力学第一法則\(~\varDelta U=\varDelta Q-p\varDelta V~\), 断熱過程\(~\varDelta Q=0~\)より
\[\begin{align}
\varDelta U+p\varDelta V&=0 \\
nC_V\varDelta T+\frac{nRT}{V}\varDelta V&=0 \\
\frac{C_V}{T}\varDelta T+\frac{R}{V}\varDelta V&=0 \\
\frac{\varDelta T}{T}+\frac{R}{C_V}\frac{\varDelta V}{V}&=0 \\
logT+logV^{\frac{R}{C_V}}&=0 \\
TV^{\frac{R}{C_V}}&=Const \\
\frac{pV}{nR}V^{\frac{R}{C_V}}&=Const \\
pV^{1+\frac{R}{C_V}}=pV^{\frac{C_V+R}{C_V}}=pV^{\frac{C_p}{C_V}}=pV^{\gamma}&=Const \\
\end{align} \]
最後の行
\[pV^{\gamma}=Const,\quad \gamma=\frac{C_P}{C_V}\tag{6} \]
これをポアッソンの関係式と呼ぶ。
ケルビンの絶対温度 理想気体の計算からも導かれる。
以前に
ケルビンの熱力学的温度を導出した。カルノー機関の効率が温度のみによることから,
\[\frac{Q_L}{Q_H}=f(T_L,T_H)=\frac{\phi(T_L)}{\phi(T_H)}=\frac{T_L}{T_H} \]
という経緯だったが, トムソン(ケルビン卿)の直感\(~\phi(T)\equiv T~\)が分り難い読者もいると思う。
一般性は欠くが, この温度と熱量の関係は理想気体の計算でも求められる。
厳密にいえば, 絶対温度を仮定した理想気体から, 絶対温度を導出しても循環論法に過ぎないが, まあ一度やってみよう。
熱力学の理論が良くできていることは実感される。
熱量の比\(~Q_H/Q_L~\)は等温過程における(1), (4)式より,
\[\frac{Q_H}{Q_L}=-\frac{T_H log\frac{V_B}{V_A}}{T_L log\frac{V_D}{V_C}} \tag{7}\]
と表される。一方カルノーサイクルの2つの断熱過程\(~B\to C~\)および\(~D\to A~\)において
\[pV^{\gamma}=\frac{nRT}{V}V^{\gamma}\Rightarrow TV^{\gamma-1}=const. \]
を適用すると
\[T_HV_B^{\gamma-1}=T_LV_C^{\gamma-1},\;T_HV_A^{\gamma-1}=T_LV_D^{\gamma-1} \]
辺々で割り算をすると,
\[\left(\frac{V_B}{V_A}\right)^{\gamma-1}=\left(\frac{V_C}{V_D}\right)^{\gamma-1}\quad \therefore \frac{V_B}{V_A}=\frac{V_C}{V_D} \]
(7)式に代入して
\[\frac{Q_H}{Q_L}=-\frac{T_H}{T_L} \]
を得る。以前の導出では, \(Q_H\gt 0,\;Q_L\gt 0~\)であるが, ここでは\(~Q_H\gt 0,\;Q_L\lt 0~\)である。クラウジウスは更に
\[\frac{Q_H}{T_H}+\frac{Q_L}{T_L}=0 \]
として, 自身が「換算熱」と呼んでいた,
エントロピーの発見へと進む。
カルノーサイクルの結果は現代でも正しいのであるが, カルノーの考えた動作は異なるものであった。熱(熱素)の量は変化せずに, 熱(熱素)が高温の場所から低温へ流れることで仕事が生み出されるとした。熱\(~\rightleftarrows~\)仕事の変換はクラウジウスの登場を待たねばならなかった。
ジュールは精力的に実験に取り組み, 仕事は熱に変え得ることを見出して, 熱素は存在しないと主張した。しかし, 当時の技術的限界もあって, 熱とは何か, 熱を仕事に変えられるかどうかは謎のままだった。
トムソン(ケルビン卿)は直感でカルノーの結果は正しいと確信したが, ジュールの「熱素は存在しない」との矛盾に悩んだ。一方, クラウジウスは, ①熱は仕事に変えられる, ②熱が低温の場所から高温の場所へ自然に流れることはない, の2点を認めれば, ジュールの説も, カルノーの理論も成り立つことを明らかにした。そしてニュートンの運動法則に匹敵する大発見, エントロピーに至る。
高温熱源に関連する「何か」\(\displaystyle \frac{Q_H}{T_H}~\)と低温熱源に関連する「何か」\(\displaystyle \frac{Q_L}{T_L}~\)を加えると保存量になる。
クラウジウスはこの「何か」を「換算熱」と呼んでいたが, 後にその重要性に気付き「エントロピー」と名付けた。
1865年, 奇しくもマックスウェルが電磁気学の集大成「電磁場の動力学」を出版した年である。