楽しく学ぶ…熱力学
ヘルムホルツの自由エネルギー(1) 電池の熱力学
ヘルムホルツ自身による自由エネルギーの導出
化学過程の熱力学 電池の化学変化と起電力から導かれた自由エネルギー。
ヘルムホルツは26歳でエネルギー保存則を打ち立てた。しかし, 生活は豊かとは言えず, 政府の援助が得られる医学の道へ進んだ。
物理学への興味が失なわれることはなかったが, 医学に関連した生理学が中心の学究生活だった。物理学への夢捨てがたく, 50歳でベルリン大学物理学教授の職を得, 1882年61歳の時に出版したのが「化学過程の熱力学」である。
この論文で(化学)
自由エネルギーの概念をギブスとは独立に提唱し, 自然の変化は自由エネルギーの減少する方向へ向かうことを示した。
ギブスが相平衡の研究からギブスの自由エネルギーに至ったのは1773年。そして371頁に及ぶ化学熱力学の金字塔『不均一な物質系の平衡に就いて』を発表したのは1876年, 1878年である。しかし, この大論文は「コネティカット学術アカデミー紀要」というアメリカの片田舎での出版でもあり, オストワルドによってドイツ語に翻訳されたのは1891年, ルシャトリエによってフランス語に翻訳されたのは1899年であった。
電池の起電力
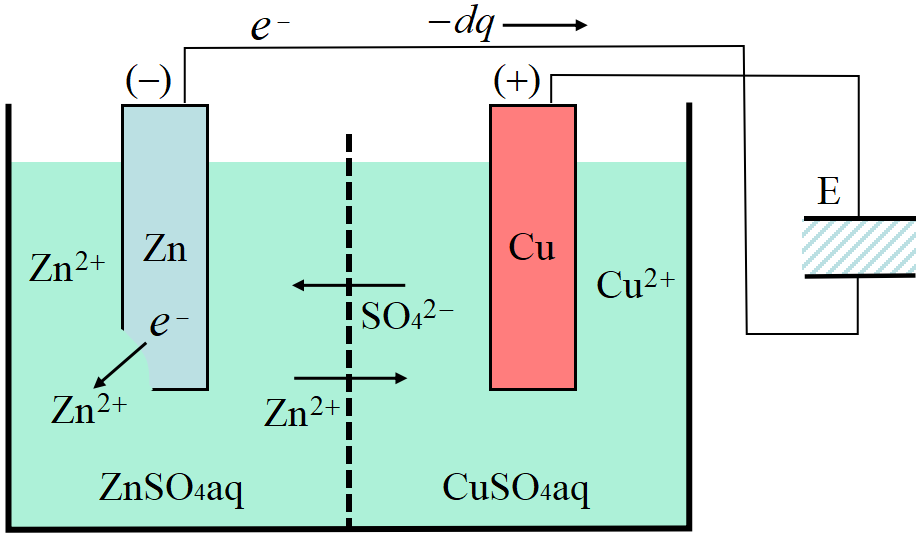
図はヘルムホルツ自身も実験に用いたダニエル電池である。起電力\(~\rm E~\)に充電された, 極めて大きなコンデンサーに接続してある。
カルノー機関では外界へ為す微小仕事は\(~d'W=pdV~\)であったが, 電池で相当するのは\(~d'W=Edq~\)である。\(dq~\)は電池がコンデンサーを充電する微小電荷である。
現代では電池の起電力を求める場合, 水素を基準とした標準電極電位から求める。例えば
\[\begin {align}
Zn^{2+}+2e^{-}=Zn\;E^0&=-0.76(\rm V)\\
Cu^{2+}+2e^{-}=Cu\;E^0&=+0.34(\rm V)\\
E=+0.34-(-0.76)&=1.10(\rm V)
\end{align} \]
標準電極電位は白金黒(黒色白金粉末)を水素電極とし, 個別の金属との電位差を精密なポテンシオメーターを用いて測定する。
詳しくは化学の教科書を参照されたい。
さて, この電池の挙動を熱力学から明かしたのがヘルムホルツである。熱機関の解析には不要であった自由エネルギーの概念が生まれる。
以下は渡辺正氏, 妹尾学氏訳, ヘルムホルツ著「化学過程の熱力学」の一部を改編・解説したものである。但し, 計算には最新のデータを使った。記号は現代風に改めてある。
電池反応の熱力学的取り扱い
温度一定のもとで電池内部に化学反応が生じ, 電気量\(~dq~\)が流れたとする。ダニエル電池の化学反応は
\[Cu^{2+}(aq)+Zn(s)\to Cu(s)+Zn^{2+}(aq);\;\varDelta H=-218.3\quad [kJ/mol] \]
の発熱反応であることが分かっている。
途中の仕切り板は\(~\rm SO_4^{2-},\;Zn^{2+}~\)イオンのみが通過し, 電気的なバランスを保つようになっている。
このとき, コンデンサーの負極板から正極板へ電気量\(~dq~\)が移動し, コンデンサーの静電エネルギーが\(~Edq~\)だけ増加する。
コンデンサーは十分大きく, 常に起電力\(~E~\)に保持されているので無限小の電流しか流れず, いわゆるジュール熱は無視して良い。
電池は平衡状態にあるので熱力学の諸法則に従うはずである。熱力学は気体の理論ではない。よく読めば, 液体, 固体に制限を加えてはいない。
体積変化は無視してよいから, \(pV~\)仕事は0で, 外界へ為す仕事は\(~Edq~\)である。温度を一定に保つために, 電池へ出入りした熱量を\(~d'Q~\)とする。
電池は等温(大気温), 定圧(大気圧)下にあり, 反応熱はゆっくり外界(大気)へ放出され等温を維持する。発熱反応では放出であるから\(~d'Q\lt 0~\)である。
しばらく終着点の見えない式変形が続く。電池反応に伴う諸現象, 起電力を熱力学変数で記述するのが目標である。目標を見失わないために, 前に戻らなくて良いよう式は繰り返し記述し, また変形は省略しないで進める。
熱力学第一法則から,
\[dU=d'Q-Edq\tag{1} \]
電池は平衡状態にあり極めてゆっくり進むので, 電池内部では電流によるジュール熱の発生はないとしてよい。
ただし電池内部の化学変化は起こるので, そのことに伴う反応熱は生ずる。等温下で相変化が起こると潜熱が系から出入りするのと同じである。
\(d'Q~\)は電池に出入りする熱量である。発熱反応の場合, 発熱した分を外界に放出し, 系の温度を一定に保つ。
出入りとは言ったが, \(d'Q(\lt 0)~\)は系から出てゆく反応熱である。化学反応式の\(~\varDelta H=-218.3\;[kJ/mol]~\)はこの\(~d'Q~\)と\(~Edq~\)の和である。
自由に取り出せるエネルギーと取り出せないエネルギーのヒントがここにある。
外部へ仕事として取り出せるのは\(~Edq~\)のみで, 反応熱は取出せない。
ただし, 低温熱浴に触れさせ, ピストンを動かせば反応熱を仕事として取り出せるが, そのような機関無しには取り出せないということである。束縛エネルギーの説明で, よく見かける「低温熱浴によってのみ取り出せる」とあるのはそういう事である。「束縛」だから取り出せないというわけではない。
電池の内部エネルギーは温度と電荷の関数, すなわち\(~U(T,q)~\)とする。クラウジウスが温度\(~T~\)と, これ以外のもう一つのパラメーターを用いて考察したのに倣っている。つまり系の自由度は2ということ。系のエントロピーを計算するために系に出入りする熱量\(~d'Q~\)に注目して,
\[\begin{align}
d'Q&=dU+Edq \\
&=\left(\dd{U}{T}\right)_qdT+\left(\dd{U}{q}\right)_Tdq+Edq\tag{2} \\
&=\left(\dd{U}{T}\right)_qdT+\left\{\left(\dd{U}{q}\right)_T+E\right\}dq\tag{3}
\end {align}\]
(3)式の両辺に
積分因子\(~1/T~\)を乗ずると,
\[dS=\frac{d'Q}{T}=\frac{1}{T}\left(\dd{U}{T}\right)_qdT+\frac{1}{T}\left\{\left(\dd{U}{q}\right)_T+E\right\}dq\tag{4} \]
一方\(~S(T,q)~\)の
全微分は
\[dS=\left(\dd{S}{T}\right)_qdT+\left(\dd{S}{q}\right)_Tdq\tag{5} \]
である。(4), (5)式を比較して,
\[\left(\dd{S}{T}\right)_q=\frac{1}{T}\left(\dd{U}{T}\right)_q,\;\left(\dd{S}{q}\right)_T=\frac{1}{T}\left\{\left(\dd{U}{q}\right)_T+E\right\}\tag{6} \]
を得る。さらに\(~dS~\)が
完全微分となる条件より, 次式が成り立つ。
\[\left\{\dd{}{q}\left(\dd{S}{T}\right)_q\right\}_T=\left\{\dd{}{T}\left(\dd{S}{q}\right)_T\right\}_q\tag{7} \]
(6)式を(7)式に代入して,
\[\begin{align}
\left\{\dd{}{q}\frac{1}{T}\left(\dd{U}{T}\right)_q\right\}_T&=\left[\dd{}{T}\frac{1}{T}\left\{\left(\dd{U}{q}\right)_T+E\right\}\right]_q \\
\frac{1}{T}\cancel{\left\{\dd{}{q}\left(\dd{U}{T}\right)_q\right\}_T}&=\frac{1}{T}\left\{ \cancel{\dd{}{T} \left(\dd{U}{q}\right)_T} +\left(\dd{E}{T} \right)_q\right\}-\frac{1}{T^2}\left\{\left(\dd{U}{q}\right)_T+E\right\}\\
0&=\frac{1}{T}\left(\dd{E}{T}\right)_q-\frac{1}{T^2}\left\{\left(\dd{U}{q}\right)_T+E\right\}\\
T\left(\dd{E}{T}\right)_q&=\left(\dd{U}{q}\right)_T+E\tag{8}
\end{align} \]
を得る。電池の起電力が, (1)式, 熱力学第一法則, (4)式, 熱力学第二法則, および純粋な数学的要請(7)式から求められるという訳である。
(8)式がギブス・ヘルムホルツの式と呼ばれるものである。正しくは, ギブス・ヘルムホルツの式には多数の表現方法があり, その一形式である。熱力学における関係式で, 内部エネルギーまたはエンタルピーと, 自由エネルギーの間の関係式である。1876年にギブスが理論的に導出し, 1882年にヘルムホルツが実験的に証明した。後で簡単に触れる。
(8)式が示すのは, 電池の起電力\(~E~\)は熱力学的に算出できるという事である。ただし, \(~\displaystyle T\left(\dd{E}{T}\right)~\)が確定するためには, \(T=0~\)での\(~E~\)の値が確定しなければならない。この辺りから「熱力学第三法則, \(Nernst~\)の定理」の必要性が生まれるのであるが。
話が横道にそれてしまった。結局, エネルギー保存則である最初の(3)式, つまり系(電池)に出入りする熱量
\[\begin{align}
d'Q&=dU+Edq \\
&=\left(\dd{U}{T}\right)_qdT+\left\{\left(\dd{U}{q}\right)_T+E\right\}dq\tag{3}
\end {align}\]
は(8)式を用いて,
\[d'Q=\left(\dd{U}{T}\right)_qdT+T\left(\dd{E}{T}\right)_qdq\tag{9} \]
と書ける。原論文には,
『(9)式右辺第2項が, 電荷\(~dq~\)をコンデンサーへ充電する際に, 温度を一定に保つために, 電池に供給しなければならない熱量(の仕事等価量*)である』と書かれているが, 筆者にとっては分かり易いものではない。(*ヘルムホルツは, 熱と熱以外の仕事を二種類の仕事等価量と呼んでいる.)
例えば\(~d'Q=dU+Edq~\)と比較して, \(\displaystyle E=T\left(\dd{E}{T}\right)_q\)として, 電池の起電力の様に思える。(次元も合っているし.)しかしそれは間違いである。
すぐ上の(3)式の\(~\{ \}~\)は外界への仕事を\(~d'W=pdV\to d'W=Edq~\)としたことによるものなので当然であるが, (9)式右辺第2項は数学的条件(完全微分)のみによるもので直感的な理解は難しい。
そこで(9)式で\(~dT=0~\)(等温反応)としてみれば,
\[d'Q=T\left(\dd{E}{T}\right)_qdq\tag{10} \]
となる。
ダニエル電池は発熱反応であるから(10)式の\(~d'Q~\)は, 外界に放出して系の温度を一定に保つ発熱量である。直感的に分かり難い(9)式右辺の第2項も同じ物理量(発熱量)であると理解できる。\(d'Q\lt 0~\)であるから, 起電力の温度係数が負であることも分かる。
ヘルムホルツが「自由に仕事に変換できない」と述べたエネルギーであるが, 概算して見よう。
ダニエル電池は2価のイオン反応であるから, 標準状態では(10)式より,
\[\begin{align}
d'Q&=T\left(\dd{E}{T}\right)_qdq \\
&=T\left(\dd{E}{T}\right)_q\x 2\x F \\
&=298\x (-1.0\x 10^{-4})\x 2\x 96485 \\
&=-5.75\quad [kJ/mol]
\end{align} \]
\(F~\)はファラデー定数で\(~96485~(\rm C/mol)~\)である。起電力の温度係数\(~dE/dT=-1.0\x 10^{-4}~\)は後述する。
反応熱\(~218.3\;[kJ/mol]~\)の2.6%は起電力としては取出せず, 系の温度を一定に保つために放出される。
ダニエル電池の起電力を計算して見よう。
\(pV~\)仕事は無いと考えてよく, 反応熱\(~\varDelta H~\)と\(~\varDelta U~\)に差はないので\(~-\varDelta H=-\varDelta U=218.3\;[kJ/mol]~\)。2価のイオン反応であるので, (8)式を電荷量を用いて\(~(\rm C\cdot volt)~\)で表す。起電力の温度係数\(~dE/dT=-1.0\x 10^{-4}\)を用いて, (8)式より,
\[\begin{align}
E&=-\left(\dd{U}{q}\right)_T+T\left(\dd{E}{T}\right)_q \\
&=\frac{-\varDelta H}{2F}+T\left(\dd{E}{T}\right)_q \\
&=\frac{218.3\x 10^3}{2\x 96485}-298\x 1.0\x 10^{-4}\\
&=1.13126-0.0298\\
&=1.10
\end{align}\]
を得る。標準電極電位から求めた, ダニエル電池の起電力\(~1.1\rm V~\)と同じ値となっている。
(筆者注:数値が一致しすぎているが, データそのものが理論値から求められたからであろう。例えば, \(\varDelta G~\)は起電力を測定して, そこから計算したのであろう。実測データを探し求めたが見つからなかったのでやむを得ない。計算の手順だけでも理解して頂ければ幸いである.)
ギブス・ヘルムホルツの式
この記事の本題ではないが, 話の都合上簡単に触れておく。
\[U=F-T\left(\dd{F}{T}\right)_V \]
\[H=G-T\left(\dd{G}{T}\right)_p\tag{11} \]
この二つの式と, これらから導かれる一連の式をギブズ-ヘルムホルツの式と呼ぶ。(by Wiki)
有名なものは, ギブスの自由エネルギーとヘルムホルツの自由エネルギーを結びつける,
\[\dd{}{T}\left(\frac{G}{T}\right)_p=-\frac{H}{T^2} \]
である。電池の起電力に関するものとして, 電池の起電力\(~\varDelta G=-zFE~\)を(11)式に代入して,
\[\varDelta H=zFE-T\left(\dd{}{T}(-zFE)\right)_p=zFE+zFT\left(\dd{E}{T}\right)_p \]
が得られる。ダニエル電池では\(~\varDelta H=-218.3\;[kJ/mol]~\), \(\varDelta G(=zFE)=-212.5\;[kJ/mol]~\)を用いて,
\[\begin{align}
-218.3\x 10^3&=(-212.5)\x 10^3+2\x 96485\x 298\x \left(\dd{E}{T}\right)_p \\
\left(\dd{E}{T}\right)_p&=\frac{-5.8\x 10^3}{2\x 96485\x 298}=-1.0\x 10^{-4}
\end{align} \]
が得られる。
ヘルムホルツの自由エネルギー ヘルムホルツは「自由\(~frie\) \(Energie~\)」という用語を提案した。
ヘルムホルツの自由エネルギーの導入
コンデンサーを充電するエネルギー\(~Edq~\)は電池の化学反応から得られるのは確かだが, 式変形だけでは, 結局\(~Edq~\)の出所(でどころ)を明確に捉えられない。もっと見通しの良い方法はないか?
さて, 電池系のエントロピー(4)式と全微分\(~dS~\)との比較で得られた, (6)式の2番目の式,
\[\left(\dd{S}{q}\right)_T=\frac{1}{T}\left\{\left(\dd{U}{q}\right)_T+E\right\} \]
を起電力\(~E~\)について解くと,
\[\begin{align}
E&=-\left(\dd{U}{q}\right)_T+T\left(\dd{S}{q}\right)_T \\
&=-\left(\dd{}{q}(U-TS)\right)_T
\end{align} \]
が得られる。そこでヘルムホルツは
\[F=U-TS\]
という物理量を導入し, この\(~F~\)が様々な重要な役割を果たすことを見出してゆく。先ずは電池の仕事能力\(~Edq~\)を求めて見よう。
電池系の熱力学第一法則を次の様に書く。
\[dU=TdS-Edq\tag{11} \]
右辺第1項は外界との熱のやり取りであり, 第2項はコンデンサーを充電するエネルギーである。
ここで先ほど得られたヘルムホルツの自由エネルギー\(~F=U-TS~\) の微小変化を取ってみると,
\[\begin{align}
dF&=dU-d(TS)\\
&=(\cancel{TdS}-Edq)-(\cancel{TdS}+SdT)\\
&=-Edq-SdT
\end{align}\]
等温変化という条件下では(元々平衡は等温で成り立つ), \(dT=0~\)だから
\[dF=-Edq\tag{12} \]
となる。\(F~\)の減少分が, コンデンサーを充電するエネルギーである。大変すっきりとした関係が得られた。
力学とのアナロジーで
\[E=-\dd{F}{q} \]
としてみると, \(F~\)をポテンシャルエネルギーと呼んでも良さそうである。
(12)式より
\(~F=U-TS~\)の減少分が, 外部へ仕事として取り出せる, 熱以外のエネルギーである。
電池の起電力となるエネルギーの源泉は\(~F~\)であり, 内部エネルギー\(~U~\)でもなければ, 反応熱\(~\varDelta Q~\)でもない。
そこでヘルムホルツは,『定温変化に対して, 関数\(~F~\)は自由に変換可能な仕事の『ポテンシャルエネルギー』の値に相当する。このため, 私はこの量を物体系の『自由エネルギー』\((frie\) \(Energie)~\)と呼ぶことを提案したい.』と主張した。
実際にはもっと多くの実験, 考察を経て『ポテンシャルエネルギー』と呼ぶ決断をしたのであろう。力学の『ポテンシャルエネルギー』には長い歴史があり, 形式が似ているというだけで勝手に命名出来るようなものではない。
\(F~\)が\(~Edq~\)のみしか表現できなければ,「自由ポテンシャルエネルギー」という名称は大袈裟である。エントロピー\(~S~\)を求めてみよう。
\(~S~\)の全微分\(~dS~\)との比較で得られた(6)式の最初の式
\[\displaystyle\left(\dd{S}{T}\right)_q=\frac{1}{T}\left(\dd{U}{T}\right)_q\]
を使うと
\[\left(\dd{F}{T}\right)_q=\dd{}{T}(U-TS)=\left(\dd{U}{T}\right)_q-S-T\left(\dd{S}{T}\right)_q=-S \]
となり, エントロピーが \(F~\)の微分から求められる。
\[S=-\left(\dd{F}{T}\right)_q\tag{13} \]
また, 内部エネルギー\(~U~\)は,
\[U=F+TS=F-T\left(\dd{F}{T}\right)_q\tag{14} \]
と, これも\(~F~\)の微分から求められる。つまり\(~F~\)は熱力学関数\(~S,\;U~\)を導くことが出来る
完全な熱力学関数である。
完全な熱力学関数\(~F~\)は, 自由エネルギーと呼ぶのにふさわしい新しい関数と言える。
\(U=F+TS~\)は従来通り「総(内部)エネルギー」と呼ぶ。(この名称もヘルムホルツの創作である.)
束縛エネルギー(\(gebundene\) \(Energie\)) それ程強い意味ではなさそうだ。
ヘルムホルツは化学過程において, 化学親和力のうちで熱としてのみ出現可能なエネルギーを束縛エネルギー\(~gebundene\) \(Energie\), 熱以外の形態に自由に変換可能な部分を自由エネルギー\(~frie\) \(Energie~\)と名付けた。熱以外と言っても, 筆者は乾電池の膨張(時々事故を起こす)と電池の起電力しか思い浮かばないが。
当時ドイツでは融解熱, 昇華等の潜熱を\(~gebundene Wärme~\)と呼んでおり, 自由にならない, 制約されたという意味が適切であろう。限定されてどうにもならない程の強い意味は無さそうである。
化学反応の反応熱は束縛エネルギーであるが, 束縛とは言っても, 蒸気機関を通せば(低温熱浴に触れさせれば)仕事をなし得るのは前述したとおりである。絶対に仕事に変換できないという訳ではない。
(14)式で, \(TS=U-F~\)としてみると, \(TS~\)は, 総エネルギーから仕事に変換可能なエネルギーを差し引いたもの, すなわち, 仕事に変換不可能なエネルギーを表し, これを「束縛エネルギー」と呼ぶことも提案した。
また,『束縛エネルギー\(~TS~\)とは, 温度\(~T~\)において物体のエントロピー\(~S~\)を生み出すために物体に取り込まなければならない熱量の力学的等価量である』とも主張している。
ここのところが分かり難いが,
具体的な例で説明しようと思う。
変化の進む方向
電池の反応は, 等温下で自発的に開始され, 外界に対して仕事\(~Edq~\)を為す。(12)式で見たように
\[dF=-Edq\tag{12} \]
自由エネルギー\(~F~\)の減少分が, 外界に為す仕事, 外界へ取り出すことの出来る仕事である。このことから
「等温下で自発的に進む化学反応は外界へ仕事を為し, 自由エネルギー\(~F~\)は減少する.」
と言える。自由エネルギーが増加する\(~\varDelta F\ge 0~\)時は\(~F~\)は最小値であり, 系は平衡状態にある。
エントロピーの大きさは『無秩序性の尺度』
現代ではエントロピーは統計的な現象で, 無秩序性の尺度であるのは誰でも知っている。しかしボルツマンが論文に著したのは1877年, 有名な\(~S=k_BlogW~\)として広く認められたのは1900年になってからである。ヘルムホルツの論文は1882年である。
現代の解釈とは若干異なるが, ヘルムホルツはエントロピーについて次の様に述べている。
『理論力学では以前から活力あるいは実エネルギーと呼ばれてきた量を, 熱の化学等価量と明確に区別するための表現を検討しておく。ただし, 後者の大部分は目に見えない分子運動のエネルギーとして解釈されるべきものである。私は, 前者を『秩序運動の活力』(\(die\) \(lebengige\) \(Kraft\) \(geordeneter\) \(Bewegung\))と呼ぶことを提案したい。ここで『秩序運動』として考えているのは, 運動している質量速度成分が空間座標の微分可能な関係とみなしうるような運動である。これに対して無秩序運動(\(ungeordenete\) \(Bewegung\))というのは, 個々の微小部分の運動が, これに隣接する微小部分の運動と全く相関を持たないようなものと考えることができる。われわれは, 熱運動が後者の分類に入ることを十分な根拠をもって信ずることができ, したがってこの意味で, エントロピーの大きさは『無秩序性の尺度』(\(Mass\) \(der\) \(Unordunung\))として解釈できる。われわれが使っている装置は分子の大きさに比べれば十分に大きいので, 規則的運動のみを他の仕事形態へ変換することができる。』
クラウジウスはエントロピーの導出に当たって, 原子の実在性を全く前提とせず,
啓蒙書などで良く使われる「デタラメさの尺度」と言った意味は全く無かった。
このヘルムホルツの論文は, エントロピーを『無秩序性の尺度』として捉えた(筆者の知る限り)最初の論文である。が本当に分かり難い。筆者の翻訳(?)は以下のようである。
同じ運動エネルギーでも, 力学における砲弾の運動エネルギーと, 化学反応における発熱量とは明確に区別する必要がある。化学反応における発熱量の大部分は目に見えない分子運動のエネルギーである。砲弾の場合は地表の座標の微分で表すことができる。そこでこれを『秩序運動の運動エネルギー』と呼ぶ。これに対して無秩序運動というのは, 全くバラバラな運動である。熱運動は隣の分子とは全く無関係な運動で「座標の微分では表せない」。そこで取り込む熱量の大きさ「エントロピー」は『無秩序性の尺度』として解釈できる。