楽しく学ぶ…熱力学
エントロピー(3) 理想気体のエントロピー
兎に角エントロピーは分り難い。習うより慣れろで, 計算して見よう!
理想気体のエントロピー変化 \(d'q/T~\)は全微分である。安心して積分しよう。
エントロピーおさらい
等温操作において, 熱が\(~\varDelta Q~\)だけ移動する時に,
\[\varDelta S=\frac{\varDelta Q}{T} \]
を
エントロピーと名付けた。そして
微小カルノーサイクルを設定して, 微分形,
\[dS=\frac{d'q_{rev}}{T}\]
を得た。熱量\(~q~\)に ' (ダッシュ)がついているのは熱量が状態量ではないこと, また\(~rev~\)としてあるのは, 状態量としてのエントロピーは可逆過程においてのみ算出されることを示している。
可逆過程に限定される理由は
周回積分 0 とポテンシャル関数で述べた通りである。周回積分が\(~0~\)であるためには, クラウジウスの不等式 = 0。すなわち, 熱の出入りは可逆過程でなければならない。
理想気体のエントロピー
それでは早速計算してみよう。理想気体では熱力学第一法則より,
\[d'q=dU+pdV=nC_V dT+\frac{nRTdV}{V} \]
である。
積分因子 1/T を乗ずると,
\[dS=\frac{d'q}{T}=\frac{nC_V dT}{T}+\frac{nRdV}{V} \]
となる。これを積分すると,
\[\varDelta S=S(B)-S(A)=\int_{A}^{B}nC_V\frac{dT}{T}+\int_{A}^{B}nR\frac{dV}{V}\]
となり
状態量\(~S\), エントロピーが算出される。\(C_V~\)が温度に依存しない場合には次の様になる。
\[\begin{align}
\varDelta S&=nC_Vlog\frac{T_B}{T_A}+nRlog\frac{V_B}{V_A}\tag{1} \\
&=nC_Vlog\frac{T_B}{T_A}+nRlog\frac{p_A}{p_B}\tag{1'}
\end{align} \]
である。(1) → (1') では, \(~p_AV_A=p_BV_B(=nRT)~\)を用いた。
等温過程 エントロピー変化は可逆過程が最大。「デタラメさ」という概念からは, 不可逆過程の方が大きい気がするが?
等温過程でのエントロピー変化は(1), (1')で\(~T_A=T_B~\)として,
\[\varDelta S_{A\to B}=S(B)-S(A)=nRlog\frac{V_B}{V_A}=nRlog\frac{p_A}{p_B}\tag{2} \]
である。\(~\varDelta S=\varDelta Q/T~\)と比べても(\(\varDelta Q=~\)系が吸収した熱量\(~=~\)系が外界に為した仕事\(~=pdV~\)),
\[\varDelta Q_{A\to B}=\int_{V_A}^{V_B}\frac{nRT_A}{V}dV=nRT_Alog\frac{V_B}{V_A} \]
\[\varDelta S_{A\to B}=\frac{\varDelta Q_{A\to B}}{T_A}=nRlog\frac{V_B}{V_A} \]
で, 当然であるが(2)式と同じである。この例からは, エントロピーの変化\(~=~\)熱の移動のような気がするが。
等温膨張で体積を2倍にすると,
\[\varDelta S=nRlog\frac{V_B}{V_A}=Rlog\frac{2V}{V}=1.38\; [cal/deg] \]
だけエントロピーが増加する。逆に体積を圧縮するとエントロピーは減少する。
等温膨張ではないが, 体積一定で, 温度を2倍にすると, \(~\overline C_V=3~\)(比熱の理論では歴史的に\(~\overline C_V=3~\)が用いられた。現代の単位系では\(~12.5~\)である.) の理想気体1モルのエントロピーは,
\[\varDelta S=C_Vlog\frac{T_B}{T_A}=3log\frac{2T}{T}=2.08\; [cal/deg] \]
だけ増加する。温度を下げればエントロピーは減少する。
可逆等温過程での計算は以上で終了だが, 厳密な可逆過程はあり得ない。
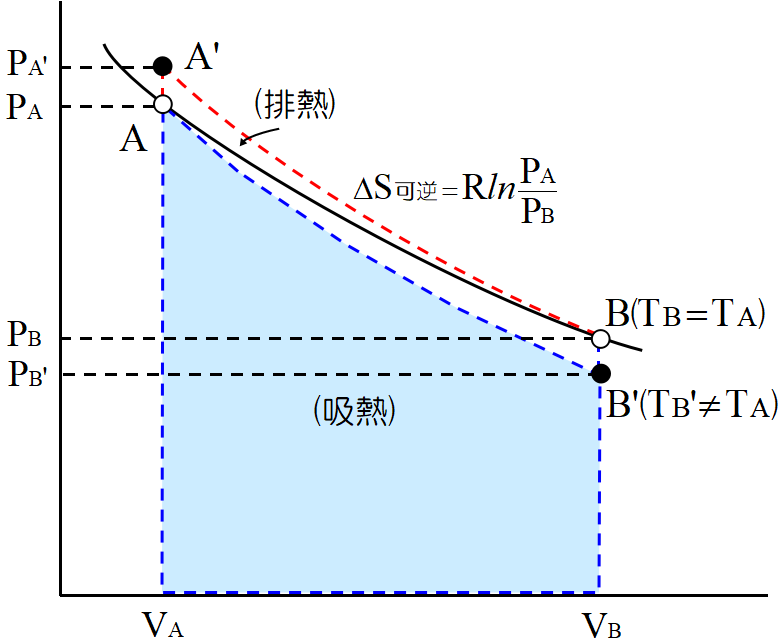
等温線\(AB~\)にそった膨張過程では, どんなにゆっくり動かしても膨張なので僅かに温度が下がり, 青破線の過程\(~A\to B\,'~\)を辿る。
青破線で囲まれた部分が, 系が外界に対して為した仕事, すなわち系が熱源から吸収した熱量である。
図から明らかに
不可逆過程で系が得る熱量は, 可逆過程より小さいことが分かる。
一方\(~B\to A\,'~\)は圧縮過程であり, 赤破線の様に僅かに温度が上がる。赤破線の下の部分の面積が外界が系に対して為した仕事, すなわち系が熱源へ放出した熱量である。
不可逆変化で失う熱量は可逆過程より大きいも明らかであろう。
\(~A\to B\,'~\)に沿った積分\(~\displaystyle \int_{A}^{B\,'}\frac{d'q}{T}~\)は可能ではあるが, 不可逆過程なので, エントロピーを与えない。単なる積分値である。
\(~A\to B\,'~\)に沿ったエントロピーは, \(B\,'~\)に至る可逆過程を見つけ, その可逆過程での積分で得られる。
\(A\to B\to B\,'~\)が\(~B\,'~\)に至る可逆過程である。
(1')式で\(~T_A=T_B~\)として, \(A\to B~\)の可逆過程(黒実線)のエントロピー変化は
\[\varDelta S_{A\to B}=nRlog\frac{p_A}{p_B}\tag{2} \]
である。不可逆過程\(~A\to B\,'~\)で
\[\varDelta S_{A\to B\,'}=nRlog\frac{p_A}{p'_B} \]
とするのは誤りである。
\(B\to B\,'~\)は定積変化なので, (1)式で\(~V_A=V_B~\)として
\[\varDelta S_{B\to B\,'}=nRlog\frac{T_B\,'}{T_B}\tag{3} \]
を得る。\(T_B\,' \lt T_B~\)であるから(3)式の値は負である。\(~A\to B\,'~\)でのエントロピー変化は, (2)+(3)であり, 当然(2)式より小さい。
このことは一般的に,
可逆過程のエントロピー変化は最大であると言える。
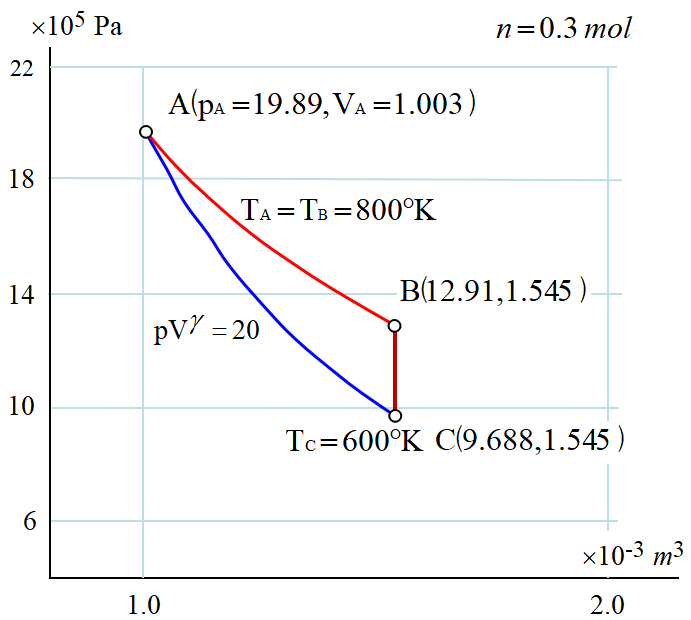
可逆断熱過程 3通りの方法で, 実際に計算して見よう!
(A) \(d'q=0~\)より(教科書には普通これしか載っていない)
\[S_{A\to C}=0\]
(B) (1)式より
\[\begin{align}
\varDelta S_{A\to C}&=nC_V log\frac{T_C}{T_A}+nR log\frac{V_C}{V_A}\\
&=nC_V log\frac{600}{800}+nR log\frac{1.545}{1.003}\\
&=0.3\x 8.314(-3/2\x 0.2877+0.4320)\\
&=0.000
\end{align} \]
(C) \(S_{A\to C}=S_{A\to B}+S_{B\to C}~\)より
\[\begin{align}
S_{A\to C}&=S_{A\to B}+S_{B\to C}\\
&=nRlog\frac{V_B}{V_A}+nC_V log\frac{T_C}{T_B}\\
&=nRlog\frac{1.545}{1.003}+nC_V log\frac{600}{800}\\
&=0.3\x 8.314(0.4320-3/2\x 0.2877)\\
&=0.000
\end{align} \]
当然であるが全て一致している。
(B)と(C)を比べると, (B)において既に\(~S_{A\to C}=S_{A\to B}+S_{B\to C}~\)となっていることが分かる。
もし\(A\to C~\)が不可逆過程ならば, 上記(C)の方法を用いて計算すれば良い。
以上の, 等温過程, 断熱過程の解析を通じて分かることの一つに, 以下がある。
カルノーサイクルにおいて, エントロピー変化は温度変化の起こらない等温過程で生ずる。温度が変化する断熱過程ではエントロピーは変化しない。
つまり, エントロピーは単純な高温から低温へ熱の移動ではない。
断熱自由膨張 \(d'q=0~\)でもエントロピーは増大する。益々エントロピーの謎が深まる。
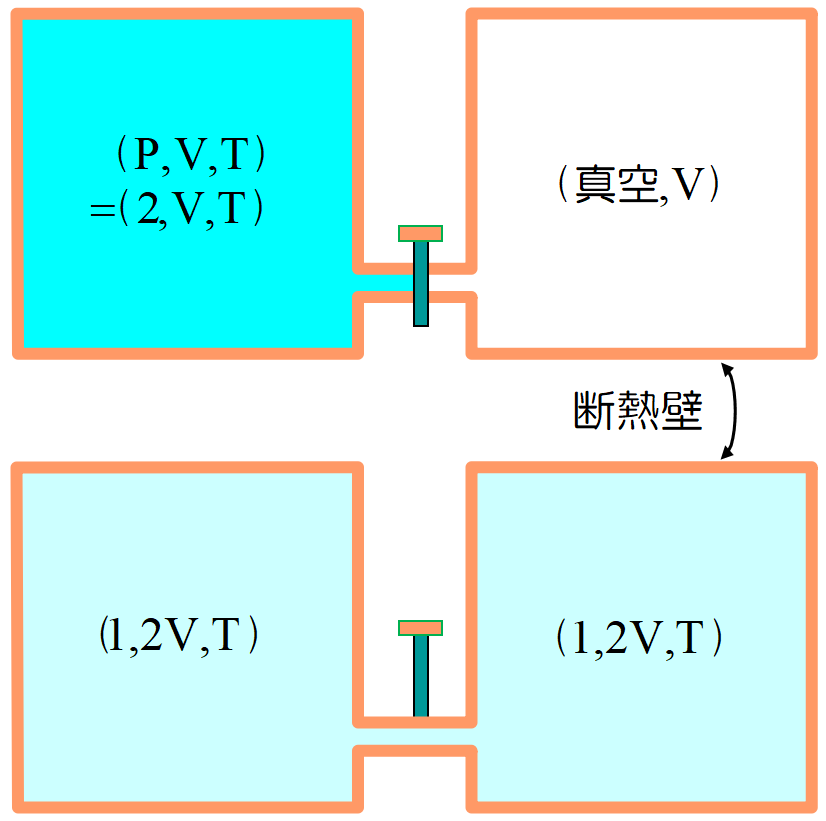
2つの断熱容器の片方(体積\(~V~\), 圧力\(2~\)気圧, 温度\(~\rm T^{\circ}K~\))に気体を満たし, もう一方(体積\(~V~\))は真空にしておく。その間にあるコックを開放すると, 気体は不可逆的に両方の容器一杯に広がる。真空に拡がる自由膨張なので仕事はせず, また断熱操作なので内部エネルギーに変化は無く, (体積\(~2V~\), 圧力\(1~\)気圧, 温度\(~\rm T^{\circ}K~\))の状態に落ち着く。
この時のエントロピー変化を求めて見よう。断熱変化で熱の流入は 0 なので, 積分\(~\displaystyle \int\frac{d'q}{T}~\)は 0 である。しかし, これはエントロピーを与えない。
断熱壁を取り払って, 温度\(~T~\)の熱源に接しながら体積\(~2V~\)まで準静的に等温膨張させると同じ状態に至る。等温変化なので, (8)式で\(~T_A=T_B~\)として,
\[\varDelta S_{rev}=nRlog\frac{V_B}{V_A}=nRlog\frac{2V}{V}=0.69nR \]
が, 断熱自由膨張におけるエントロピー変化(増大)である。
もっとも, 自由膨張でも, \(~V\to 2V~\)が唯一の変化なので, 形式的に
\[\varDelta S_{irrev}=nRlog\frac{2V}{V}=0.69nR \]
としても同じ結果が得られるが, 特殊な例である。
前述した等温膨張の場合では \(~\displaystyle \frac{p_A}{p_{B\,'}}\gt \frac{p_A}{p_B}~\)であり, 形式的に\(~\displaystyle \frac{p_A}{p_{B\,'}}~\)を代入すると, 可逆変化の\(~\varDelta S~\)より大きな値になってしまう。
自由断熱膨張でエントロピーが増大する例からも,
エントロピーの変化を, 熱の移動に求めることは間違いであることが分かる。
さらに, カルノーサイクルにおいて, エントロピーの変化は温度の変化の無い等温過程であって, 温度が変化する断熱過程ではエントロピーは変化しない。
エントロピーの本質が単なる高温から低温への熱の移動ではないことも分かる。