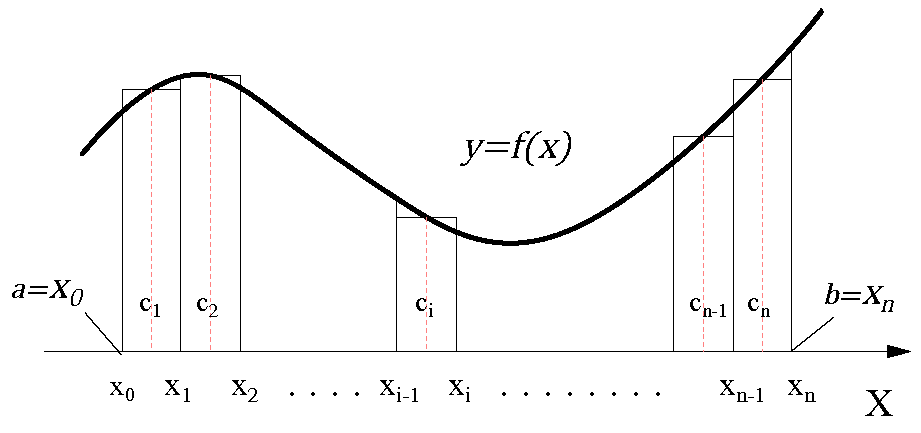
・\( \b{m_i}=\)\(inf \{f(x)\ |\ x_{i-1}≤x≤x_{i}\}\) :➁
・\(\b{M_i}=\)\(sup \{f(x)\ |\ x_{i-1}≤x≤x_{i}\}\) :③
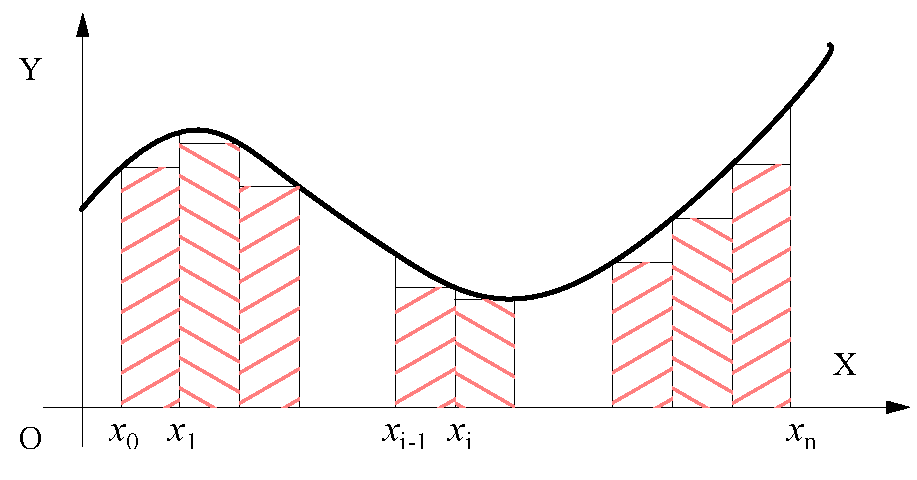
・\(\b{s(\Delta)}\)\(=\displaystyle \sum_{i=1}^{n} m_i (x_{i}-x_{i-1})\)\(=\displaystyle \sum_{i=1}^{n} m_i \Delta_i\):④
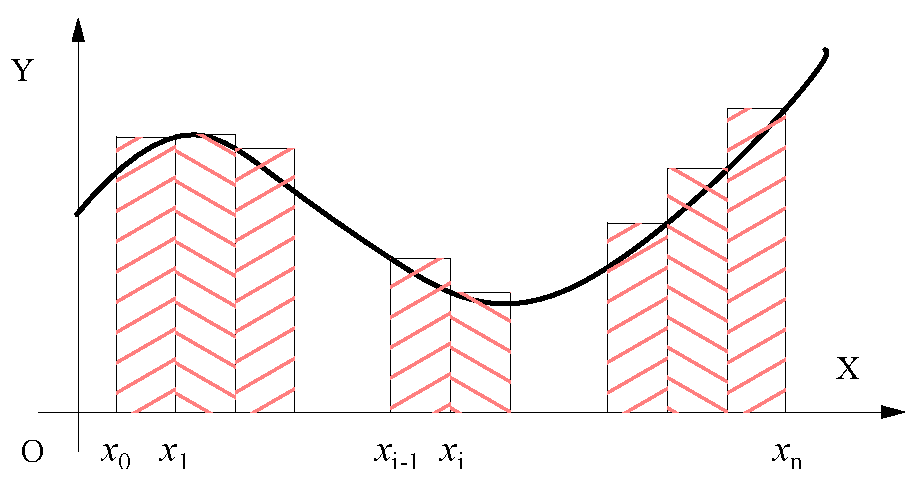
・\(\b{S(\Delta)}\)\(=\displaystyle \sum_{i=1}^{n} M_i (x_{i}-x_{i-1})\)\(=\displaystyle \sum_{i=1}^{n} M_i \Delta_i\):⑤
もし
\( \displaystyle \lim_{ |\Delta| \to 0 } s(Δ)= \displaystyle \lim_{ \Delta \to 0 } S(Δ)\) なら
はさみうちの原理より
\( \displaystyle \lim_{ |\Delta| \to 0 } s(Δ)\)\(= \displaystyle \lim_{ |\Delta| \to 0 } S_r(Δ)\)\(=\displaystyle \lim_{\Delta \to 0 } S(Δ)\) となる。
分点を増やすと、\(s(\Delta)\) と \(S(\Delta)\) は互いに近づく。
\(\Delta\) はいくらでも細かくなるので、どこかで\(s(\Delta)=S(\Delta) \) となるのではと推測する。
それを確認するのが、ここでの目的です。
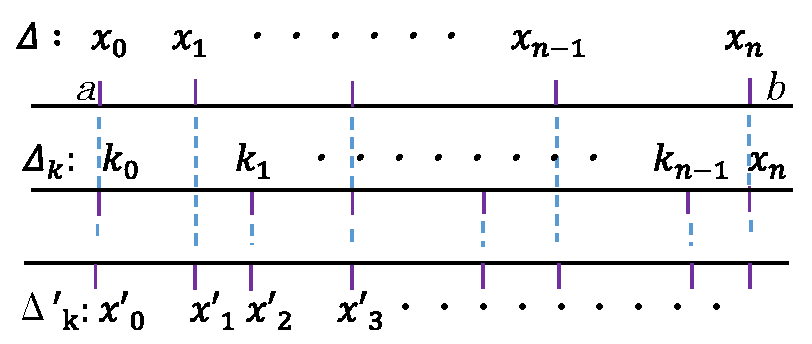
分割\(\Delta\):
\(\ (a=)x_0<x_1<x_2<…x_i<\) \(…x_{n-1}<x_n(=b)\)
に対し分点を1つ増やした分割を\(\Delta'\)分割と表す。
\(\Delta\)\(:\cdots, x_i,\ x_{i+1}\ ,\cdots\) に対し
\(\Delta'\)\(:\cdots, x'_i,\ \color{red}{x'_*}\ ,x'_{i+1},\cdots\) となる。
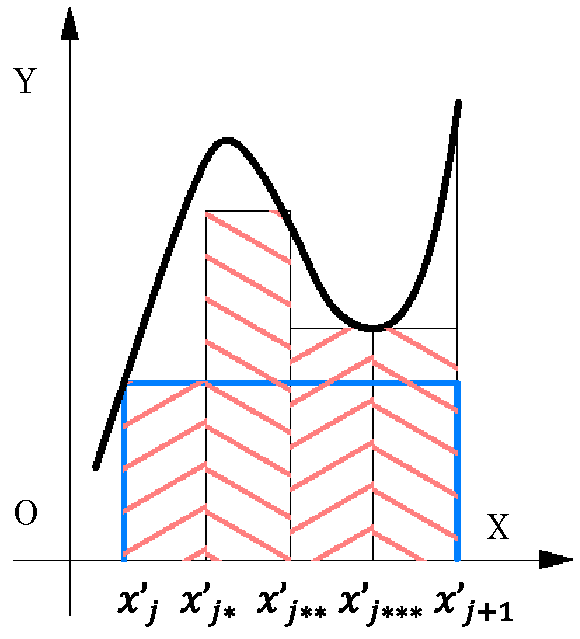
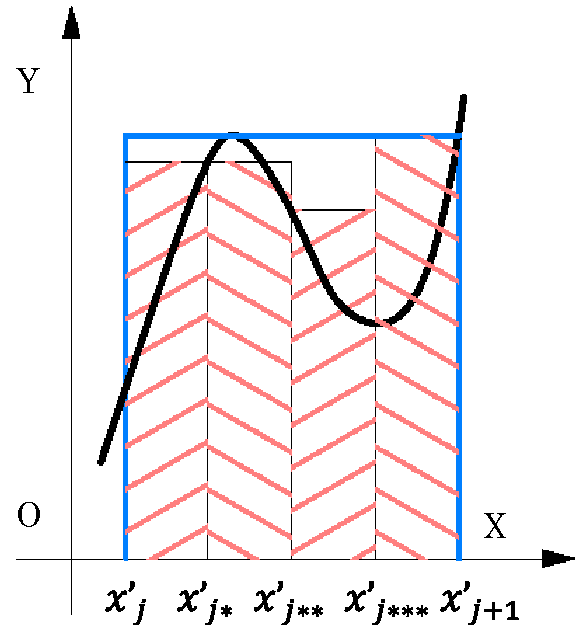
不足和は細分化後の面積は増加:\( s(\Delta)≤s(\Delta')\)
過剰和は細分化後の面積は減少:\( S(\Delta)≥S(\Delta')\)
これからの証明流れは:
Δ分割の細分により、\(s(\Delta) は下から単調増加し上限に収束、また \ S(\Delta)\) は上から単調減少していき下限に収束、その収束値が一致すると推定できる。
この一致がリーマン積分ではないかと考えられる。
\(\displaystyle \lim_{ |\Delta| \to 0 } s(Δ)\)\(=sup\ s(\Delta)=s_u \):❶
\(\displaystyle \lim_{ |\Delta| \to 0 } S(Δ)\)\(=inf\ S(\Delta)=S_ℓ\):❶'
・\(s(Δ_k)\)は分割\(Δ_k\)による不足和
・\(ε'=\frac{ε}{2}\)とする。
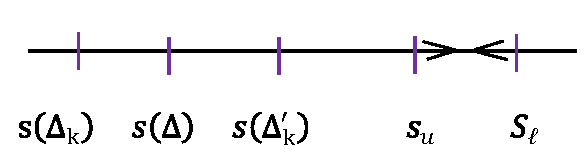
\(s(Δ) \le s(Δ'_k)\) :❸ \(\quad\) \(s(Δ_k) \le s(Δ'_k)\) :❹
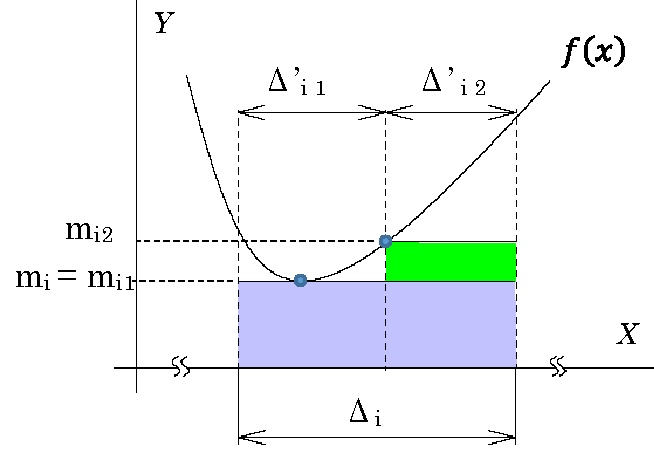
\(\delta s=(m_{i1} Δ'_{i1} + m_{i2} Δ'_{i2})\)\(-m_i(Δ'_{i1}+Δ'_{i2})\)
\(=(m_{i1}-m_i)Δ'_{i1} + (m_{i2}-m_i)Δ'_{i2}\)\(\le (M-m)Δ_i \)\(\le (M-m)Δ\)
\(\therefore \delta s \le (M-m)Δ \)
\(|s(Δ)-s_u|\)\(=s_u-s(Δ)=[s_u-\cancel{s(Δ_k)}]\)\(-[\cancel{s(Δ'_k)}-\cancel{s(Δ_k)}]\)\(+[\cancel{s(Δ'_k)}-s(Δ)]\)
\(\le (ε'-0+ε')=2ε'=ε\)
(\(s(Δ)\)は\(s_u\)に収束する)
\(\therefore s(Δ)=s_u\)
\( \displaystyle \lim_{ |\Delta| \to 0 } s(Δ)= \int_a^b f(x) dx \) \(:❻\)
\( \displaystyle \lim_{ |\Delta| \to 0 } S(Δ)= \int_a^b f(x) dx \) \(:❼\)
❻、❼から
\( \displaystyle \lim_{ |\Delta| \to 0 } s(Δ)=\displaystyle \lim_{ |\Delta| \to 0 } S(Δ)\)\(:❽\)
\(\displaystyle \sum_{i=1}^n f(c_i)Δ_i\)\(-\displaystyle \sum_{i=1}^{n} m_i \Delta_i \)
\(\lt \displaystyle \sum_{i=1}^n \frac{ε'}{b-a}(x_i-x_{i-1})\)
\(S_r(\Delta)-s(\Delta)\)\(\lt \frac{ε'}{b-a} \displaystyle \sum_{i=1}^n (x_i-x_{i-1})\)
\(=\frac{ε'}{b-a} (b-a)=ε'\)
右辺の∑の各項はキャンセルされ、残る項はb\(=x_n\)とa\(=x_0\)となる。
\(S_r(\Delta)-s(\Delta)\)\(\lt ε'\)
\(\underline{\int_a^b f(x) dx-s(Δ)}\)\(\le [\cancel{S_r(\Delta)}-s(\Delta)]\)\(+[\int_a^b f(x)-\cancel{S_r(\Delta)}]\)
\(\lt ε'+ε'=2 ε'=\underline{\ ε\ }\)
\(\therefore \displaystyle \lim_{ |\Delta| \to 0 } s(Δ)= \int_a^b f(x) dx \)
(不足和の極限は定積分S に収束する。)(式❻の成立)
\(\displaystyle \lim_{ |\Delta| \to 0 } S(Δ)= \int_a^b f(x) dx \)
(過剰和の極限は定積分S に収束する。)(式❼の成立)
式❻、❼の成立をもって下式が得られる。
\(\therefore \displaystyle \lim_{ |\Delta| \to 0 } s(Δ)=\displaystyle \lim_{ |\Delta| \to 0 } S(Δ)\) :❽
| \( \begin{array}{c|c|c|c} \hline ダルブーの定理 & 式❻、❼ & ダルブーの定理 \\ \hline \displaystyle \lim_{|\Delta| \to 0 } s(Δ)=&\int_a^b f(x) dx &=\displaystyle \lim_{|\Delta| \to 0 } S(Δ) \\ \Updownarrow & & \Updownarrow \\ sup\ s(Δ)=s_u& & inf\ S(Δ)=S_l \\ \hline \end{array} \) |
\( \displaystyle \lim_{ |\Delta| \to 0 } s(Δ)= \displaystyle \lim_{ \Delta \to 0 } S(Δ)\) なら
\( \displaystyle \lim_{ |\Delta| \to 0 } s(Δ)= \displaystyle \lim_{ |\Delta| \to 0 } S_r(Δ)=\displaystyle \lim_{\Delta \to 0 } S(Δ)\)
となる。
\(\displaystyle \lim_{ |\Delta| \to 0 } s(\Delta)\)
\(=\underline{\int_a^b} f(x) dx\)
を下積分
\(\displaystyle \lim_{ |\Delta| \to 0 } S(\Delta)\)
\(=\overline{\int_a^b} f(x) dx\)
を上積分
\(\displaystyle \lim_{ |\Delta| \to 0 } s(Δ)=sup\ s(\Delta)\) \(\ , \)
\(\displaystyle \lim_{ |\Delta| \to 0 } S(Δ)= inf\ S(\Delta)\)
( \(sup\ s(Δ)=s_u\)\(\ , \) \(inf\ S(Δ)=S_l\) )
リーマン積分を呼び起こすと:
\(S=\displaystyle \lim_{ |Δ| \to 0 } \displaystyle \sum_{i=1}^n f(c_i) (x_i-x_{i-1})\)であり、
\(\underline{s_u=S_l}\) であるとき
\( S=\underline{\int_a^b} f(x) dx\)\(=\overline{\int_a^b} f(x) dx\)\(=\displaystyle \int_a^b f(x) dx\)
これより、\(s_u=S_l\) は関数\(f(x)\) の積分可能の必要十分条件となります。
