楽しく学ぶ…熱力学
エンタルピー
3通りの名称。熱関数, エンタルピー, カマーリング・ネオスの自由エネルギー。
エンタルピー 定圧過程での熱量\(~d'Q~\)と言うだけのことだが!
不完全微分関数を完全微分関数に変換する。
熱機関の解析には不要であったエンタルピーはギブスによって導入された。ギブスは「定圧熱関数」と呼んでいた。
真価を発揮するのはギブスの自由エネルギーと組み合わせたときの化学反応熱であるが, 先ずは教科書通りの説明をしよう!
定積下での変化は, 理論計算には適しているが, 実験は中々難しい。炎天下でレールを曲がらないようにするのはほぼ不可能である。
大気圧下, 一定温度というのが最もありふれた条件であり, 定圧下での変化が最も多く見られる現象である。
定圧下で状態が\(~A\to B~\)と変化する時, 内部エネルギーの変化は
\[\begin{align}
\varDelta U&=\varDelta Q-p\varDelta V \\
U_B-U_A&=\varDelta Q-p(V_B-V_A) \\
\varDelta Q&=(U_B+pV_B)-(U_A+pV_A)
\end{align} \]
ここでエンタルピーを
\[H\equiv U+pV \]
と定義すると,
\[\varDelta Q=H_B-H_A=\varDelta H \]
すなわち, \(\varDelta H~\)は定圧下で, 系へ流入する熱量\(~C_p\varDelta T~\)を表す。ギブスが「定圧熱関数」と呼んだ所以である。
これだけのことであれば, わざわざ新しく「エンタルピー」を導入する必要は無さそうだが?
熱機関の効率を求めている間は, エンタルピー\(~H~\)は曖昧な使われ方をしており, 用語も確定していなかった。
ギブスが熱力学を「平衡系の熱力学」に応用し始め, 状況が変わった。事実, 明確に定義されたのは, ギブスの自由エネルギー1873年, ヘルムホルツの自由エネルギー1882年, エンタルピーはさらに遅れて1909年であった。
熱力学関数の解説では, \(U~\)から一回のルジャンドル変換で得られる, \(F, \;H~\)が先に取り上げられるが, 歴史的には上に述べた通りである。
それでは, 形式的ではあるがきちんと(\(\varDelta,\,d',\, d~\)を区別して)定義してみよう。話の都合上「比熱から」。
理想気体の状態方程式から分かる通り, 熱力学的な状態変数の自由度は2つしかない。そこで, 内部エネルギー\(~U~\)を\(~U(T,V)~\)とすると,
\[dU=\left(\dd{U}{T}\right)_V dT+\left(\dd{U}{V}\right)_T dV \]
となる。このとき等積変化\(~dV=0~\)であるならば, 熱力学第1法則は, \(~dU=d'Q~\)と書けるので, 熱容量は
\[C_V=\left(\frac{d'Q}{dT}\right)_{V=const}=\left(\frac{dU}{dT}\right)_{V=const}
=\left(\dd{U}{T}\right)_V\]
でこれを「定積比熱」と呼ぶ。ここで,
\[H\equiv U+pV\tag{1} \]
と定義する。これは状態量の組み合わせで作ったものであるから, 状態が決まればただ一通りに値が決まる。つまりこれも新しい状態量である。
この微小変化は
\[dH=dU+pdV+Vdp\tag{2} \]
である。定圧条件下では\(~dU=d'Q-pdV~\)より, \(d'Q(=dU+pdV)~\)は全微分であり,
\[d'Q=H_B-H_A=dU+pdV=dH \]
と, 状態量として表現出来る。つまりエンタルピー\(~H~\)は,
非状態量である熱量\(~Q~\)を, 定圧条件下で, 他の状態量と同様に取り扱えるように工夫したものである。
例えば定圧比熱は,
\[C_p=\left(\frac{d'Q}{dT}\right)_{p=const.}=\left(\dd{H}{T}\right)_p \]
(2)式で\(~dp=0~\)だから
\[C_p=\left(\dd{H}{T}\right)_p=p\left(\dd{V}{T}\right)_p \]
と表すことが出来る。
定積比熱が内部エネルギーで定義されたように, 定圧比熱は新しい状態量, エンタルピーを用いて定義できる。
不完全微分である
熱が, 状態量になり, 完全な熱力学関数になる様子はキツネにつままれたような気がしないでもない。
ただし物理的な意味は「\(\varDelta H~\)は定圧下で, 系へ流入する熱量\(~C_p\varDelta T~\)を表す」だけで, 目新しいものでは無い。
エンタルピーは簡単な概念であると言われる所以である。古い教科書では「含熱量」と言うそうである。
ギブスの考えたエンタルピー 熱力学ポテンシャルの一つ。
以上少々自嘲的に書いたが, ギブスの捉え方は少し異なるようである。
平衡状態曲面で触れたように, 三相平衡(固相, 液相, 気相)では\(~G_0~\)が一定値(=極小値)を取るように状態が変化する。\(F_0~\)も\(~H_0~\)も, 条件付きではあるが\(~G_0~\)と同じ働きをしている。
力学では系はポテンシャルエネルギーの小さくなる向きに力を受け, ポテンシャルエネルギーの減少分だけ動力を生んだ。
ヘルムホルツの自由エネルギーでは
「ヘルムホルツの自由エネルギーの減少分だけ仕事が取り出される」のであった。
こうしてみると, \(G,\;F,\;H~\)は力学に於ける「ポテンシャルと同じ働きをしている」。それで内部エネルギー\(~U~\)と共に「熱力学ポテンシャル」と呼ぶのは, 誠に適切であると言える。
熱力学ポテンシャルは完全な熱力学関数とも呼ばれ,「他の熱力学状態量を全て導出できる関数」と定義されている。厳密な数学的証明は必要ではある。
これらの熱力学ポテンシャルは, 状態が平衡点に向かうとき, 極小値に向かう。ということは全ての熱力学状態量を内包しているということであり, 数学的に証明しなくとも分かることでもある。
ところで\(~dU=d'Q~\)とか\(~dH=d'Q~\)を不可解に思う読者がいるかもしれない。状態量でない\(~d'Q~\)が, 状態量である\(~dU~\)とか\(~dH~\)に等しい。
元々状態量でないとは, 複数の経路で異なった値を取る物理量の事であった。定圧条件でも, 定積条件でも何でも良いから, 変化の経路を一通りに制限すれば状態量となるのである。
化学反応での応用 化学反応では大変重宝されるが?
さて状態量ではない\(~d'Q~\)が状態量である\(~dH~\)で表されるのは便利そうであるが, どのような使われ方をするのであろうか?
ある系がピストン内で化学反応を起こしたとき, 反応に伴う熱は,
\[d'Q=dU+pdV \]
\(dV=0\)ならば, \(dU~\)は「系の外で観測される熱量」と対応させられるが, \(dV\neq 0\)の場合が多く, 対応が難しい。そこで,
\[H\equiv U+pV \]
と定義すると, 化学反応は一般にはビーカー内(大気圧下)なので\(~dp=0~\)より
\[dH=dU+pdV+Vdp=d'Q+Vdp=d'Q\]
となり前述した通りである。
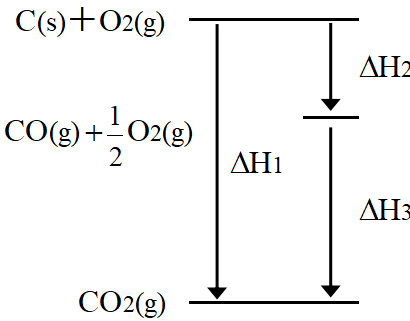
例えば高校化学の教科書に書いてある「ヘスの法則」である。図は固体の炭素を燃焼させて炭酸ガスを得る反応である。
途中の一酸化炭素の生成熱(燃焼熱)は, 周りに酸素ガスが十分あり反応が進んでしまうので, 測定は困難である。
一般には, 熱量\(~\varDelta Q~\)は状態量では無く, 反応の経路により異なる値を取る。始状態と終状態の差\(\varDelta Q~\)の足し算,引き算で正しい結論は得られない。
\[\begin{align}
&\varDelta H_1=393.5KJ/mol \\
&\varDelta H_3=283.0KJ/mol
\end{align}\]
ここで, 反応は大気圧下\(~dp=0~\)で進むので\(~\varDelta Q=\varDelta H~\)は状態量であり,
\[\varDelta H_2=\varDelta H_1-\varDelta H_3=393.5-283.5=110.5KJ/mol\]
と求めることが出来る。めでたく
ヘスの法則が正しいことが保証されるのである。
と書いたが, 如何にもこじつけの感がしないでも無い。ヘスの法則が1840年に発表されて以来, その真偽が議論されたようには思えない。やはり, 何も「エンタルピー」と名付けるほどの事はないのでは?
確かに反応熱より, 反応エンタルピーの方がそれらしく聞こえるが!筆者の理解不足か?