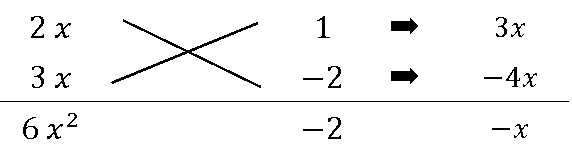与えられた式をその因数(約数)の積の形に表すことを因数分解といいます。
また、 式 A を 2つの数 a、b の積で表すとき(\(A=a \times b\))、この a, b はA の因数です。
簡単な因数分解は次のように共通因数でくくる式です。
\(ab+ac=\ul{a\ }(b+c)\)
\(2a^2x+4ax^2\)\(=\ul{2ax}\ a+\ul{2ax}\ 2x\) \(=\ul{2ax} (a+2x)\)
因数分解とは、次の例のようにある式を因数の積の形に変形することです。
\(ax^2+bx+c \rightarrow\)\(\b{(x-α)(x-β)}\)
これから2次式の因数分解の方法を、後半では高次式についてを説明していきます。
また末尾に公式(一覧)を載せておきます。
推測・直感 による
2次一般式 \(ax^2+bx+c \longrightarrow\)\((x+\Box)(x+\triangle)\)の形にする。
例題1
\(x^2+3x+2 \)
:①
□=3, △=1 と推定して、与式に因数分解は\( (x+2)(x+1) \)
確認:
\( (x+2)(x+1)\) \(=x^2+(2+1)x+2\cdot1\) \(=x^2+3x+2 \)
この例は□=2, △=1 の2つを決めるだけなので簡単でした。
たすき掛けによる方法
2次 一般式 \( ax^2+bx+c \) は 式①と比べ 推定する数が増えるので、一般的に「たすき掛け」方法を使います。
\( ax^2+bx+c \)を次のように分解します。
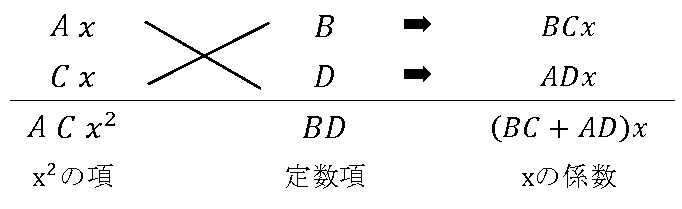
\((Ax+B)(Cx+D)\)\(=ACx^2+(AD+BC)x+BD\)
以下のA,B,C,D を推定/直感しますが、まずはAとBを推定します。
「たすき掛け」は下図のようにして考えます。
それでははじめましょう。
例題2
\(\ 6x^2-x-2 \)
\(\s{(Ax+B)(Cx+D)}\) \(\leftrightarrow\) \(\sc{=ACx^2+(AD+BC)x+BD}\)
1st:
まずA=2、C=3と推定してみる。
(A=1、C=6 だと x の係数項、定数項が成立しません)
2nd:
あと,B,Dの値を xの係数項=-1、定数項が=-2 になるような値に決める
B=1,D=-2となります。
\(\sc{ACx^2+(AD+BC)x+BD}\) \(\rightarrow\)\(\s{(Ax+B)(Cx+D)}\)
すなわち\((2x+1)(3x-2)\)となります。
確認:
\( =6x^2+(-4+3)x-2\) \( =6x^2-x-2 \)
2次方程式の解の公式により求める。
2次式 \( y=ax^2+bx+c=0 \ \) について解の公式
\(\cl{α,β}=\s{\dsfr{-b \pm \sqrt {b^2-4ac}}{2a}} \) \(\quad \sc{❶}\)
を使うと,以下がその因数分解です。
\(y=a(x-\cl{α})(x-\cl{β})\)\(\quad \sc{❷} \)
上の(1)(2)を公式(A)を使って求めてみましょう。
例題3
\( 2x^2+8x+6\)
公式❶を使い
\(α,β =\s{ \dsfr{-8 \pm \sqrt{ 64-4 \cdot 2 \cdot 6} }{4} } \)
\(=\s{ \dsfr{-8 \pm \sqrt {16}}{4} }\)
\(=\s{ \dsfr{-8 \pm 4}{4} }\)
\(α=\sc{ \dsfr{-4}{4} }\)\(=\s{-1}\)
\(β=\sc{ \dsfr{-12}{4} }\)\(=\s{-3}\)
\(α=-1,\ β=-4 \)
公式❷に代入し
\(2(x+1)\ (x+3)\)
\(\therefore(2x+2)\ (x+3)\)
例題4
\( x^2+x-12 \)
公式❶を使い
\(α,β =\s{ \dsfr{-1 \pm \sqrt{1-4 \cdot 1(-12)} }{2} } \)
\(=\s{ \dsfr{-1 \pm \sqrt {49}}{2} }\)
\(=\s{ \dsfr{-1 \pm 7}{2} }\)
\(α=3,\ β=-4 \)
公式❷に代入し
\(\therefore (x-3)(x+4) \)
例題5
\(\ 6x^2+7x+2\)
公式❶を使い
\(α,β =\s{ \dsfr{-7 \pm \sqrt{49 - 4\cdot 6\cdot 2 } }{2\cdot 6} } \)
\(=\s{ \dsfr{-7 \pm \sqrt {1}}{12} }\)
\(=\s{ \dsfr{-7 \pm 1 }{12} }\)
\(α=\sc{ \dsfr{-6}{12} }\)\(=\sc{ \dsfr{-1}{2} }\)
\(β=\sc{ \dsfr{-8}{12} }\)\(=\sc{ \dsfr{-2}{3} }\)
公式❷に代入し
\(6(x+\s{\dsfr{1}{2}}) (x+\s{\dsfr{2}{3}}) \)
\(=2(x+\s{\dsfr{1}{2}})\ 3(x+\s{\dsfr{2}{3}})\)
\(\therefore(2x+1)\ (3x+2)\)
例題6
\(\ x^2-10x+25\)
公式❶を使い
\(α,β =\s{ \dsfr{10 \pm \sqrt{100 - 4\cdot 1\cdot 25 } }{2} } \)
\(=\s{ \dsfr{10 \pm \sqrt{0} }{2} }\)
\(=\s{ \dsfr{10}{2}}\)\(=5\)
公式❷に代入し
\(\therefore (x-5)^2\)
例題7
\(\ x^2-2x+4\)
公式❶を使い
\(α,β =\s{ \dsfr{2 \pm \sqrt{4 - 4\cdot 1\cdot 4 } }{2} } \)
\(=\s{ \dsfr{2 \pm \sqrt{-12}}{2} }\)
\(=\s{ \dsfr{2 \pm \sqrt{12}i}{2} }\)
\(=\s{ \dsfr{2 \pm 2\sqrt{3}i}{2} }\)
\(α=\s{ \dsfr{2 + 2\sqrt{3}i}{2} }\)\(=1+\sqrt{3}i\)
\(β=\s{ \dsfr{2 - 2\sqrt{3}i}{2} }\)\(=1-\sqrt{3}i\)
公式❷に代入し
\(\therefore [x-(1+\sqrt{3}i)][x-(1-\sqrt{3}i)] \)
判別式による判断
\(\sc{ α,β=\dsfr{-b \pm \sqrt {b^2-4ac}}{2a}} \) \(\sc{ \quad ❶}\)
公式❶の中の次の式 \(\ul{D}\)
を判別式といいます。
\(\ul{D=b^2-4ac}\) \(\sc{\quad ❸} \)
\(D\)の値から次のことがいえます:
1)\(D\gt 0\):実数 (例題3~5) (※)以下詳細説明
2)\(D=0\) :実数の重根 (例題6)
3)\(D\lt 0\):複素数 (例題7)
(※):実数のときの補足:
実数では無理数の入るので領域を狭める
因数分解の領域の定義が有理数のとき:
ⓐ\(D\)が平方数(1,4,9,16…)である。
ⓑ\(\frac{-b}{2a}\)が有理数\(\frac{整数}{整数}\)である。
ⓐⓑが成り立つこと。
☞判別式
【参照先】
\(x^2-2x+4\)
例題7 では2次方程式の解は\(1 \pm \sqrt{3}i\)の虚数解でした。
この与式の曲線は x軸 との共有点を持たない関数です。
一般に虚数のときには, 因数分解できないというのが一般的です。
(出題者の意図する範囲(整数,有理数,実数,複素数(虚数))によります)
高次式の因数分解
高次式の因数分解は場合により解法する方法があります。
2次を超える方程式のには「2次方程式の解の公式」ようようなものはありません。
3次方程式の解の公式は一般的ではありませんが、あることはありますが、かなり複雑・特殊なので…対象から外します。
5次方程式は存在しません。
因数分解 (末尾) の公式一覧を使う方法
--時間に余裕の方にはよいですね--
例1:\(x^3+8\) のとき \(x^3+2^2\) に変形すれば, 以下の公式が使える。
「公式 \( x^3+a^3\) \(=(x+a)(x^2-xa+a^2)\) 」
式の変形・展開で解く方法
例1:\(\cl{x^3-2x^2 } \clb{ - 9x+18}\)
\(= x^2\ul{(x-2)}-9\ul{(x-2)}\)
\(= \ul{(x-2)}(x^2-9)\)
\(= \ul{(x-2)}(x+3)(x-3)\)
例2:\(x^4-2^2\) :この式を
複2次式と呼ぶ
xの次数が偶数のみで構成される多項式のこと
因数分解できる期待が高い。
次のように\(\s{(αx)^2-(βx)^2}\)の形に持ち込む。
手慣れた手法となるが,「\((2x)^2\)を足して引く」
\(=\ul{x^4-(2x)^2+2^2}-(2x)^2\)
\(=(x^2-2)^2-(2x)^2\)
この式は和と差の掛け算になる
\(\s{(A)^2-(B)^2=(A+B)(A-B)}\)
\((\ul{x^2-2}+2x)(\ul{x^2-2}-2x)\)
置き換えの方法
例1:\(x^4-2x^2-15\) :
複2次式
\(=X^2-2X-15\) \(=(A-5)(A+3)\)
A→x に戻す
\(=(x^2-5)(x^2+3)\)
因数定理と組立除去
☞因数定理【参照先】
☞組み立て除法【参考先】
因数定理とは:
\(f(x)=a_1x^n+a_2x^{n-1}\cdots a_{n-1}x+a_n\)について
多項式\(f(x)\)は\(f(a)=0\)となるとき\((x-a)\)の因数をもつ。
すなわち、\(f(a)=0\)なる a を探せば、多項式は\((x-a)\)で割り切れる。
参考) 因数の見つけ方
\(a=\pm \frac{定数項 a_n の約数}{最高次 a_1 の約数}\)\(\ \sc{:❹}\)
例:\(a_n=3, a=2\)のとき, \(a=\frac{3の約数}{2の約数}\)
因数は次の候補のいずれかといわれている。
\(a=\pm 1, \pm 3, \pm \frac{1}{2}, \pm \frac{3}{2} \)
さっそく求めてみよう
例題8:\(f(x)=x^3+x^2-x-1\)
式❹を使い(直感でもよい)
\(f(a)=0\)となる a を探すと\(a=-1\) である。
これより因数は \((x+1)\) である。
\(f(x)\) は\((x+1)\) で割り切れる。
\((x^3+x^2-x-1)÷(x+1)\)
除算→組み立て除法の結果【参照先】より
\(=x^2+2x+1\)
\(=(x+1)^2\)
\(\therefore f(x)=(x+1)(x+1)^2\)