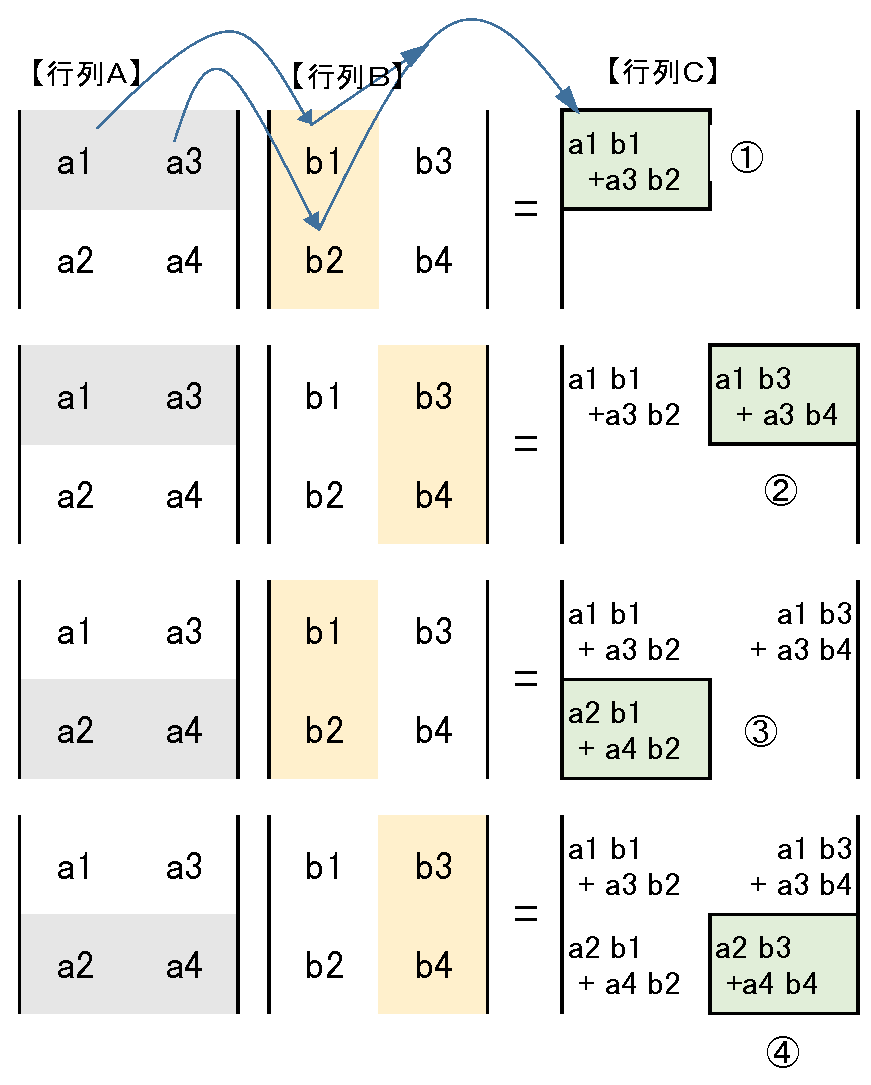
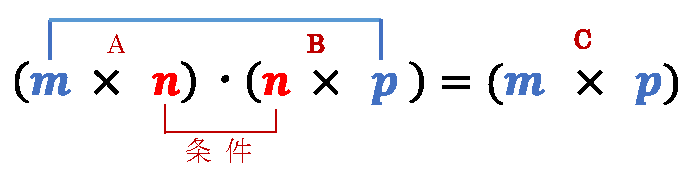上図の積の 一般式表記 は:
\(
\begin{pmatrix}
a1& a3\\
a2& a4
\end{pmatrix}
\)
\(
\begin{pmatrix}
b1& b3\\
b2& b4
\end{pmatrix}
\)
\(=
\begin{pmatrix}
a1b1+a3b2& a1b3+a3b4\\
a2b1+a4b2& a2b3+a4b4
\end{pmatrix}
\)
(1)
\(
\begin{pmatrix}
3& 2\\
2& 1
\end{pmatrix}
\)
\(
\begin{pmatrix}
1& 2& 0\\
2& 1& -1
\end{pmatrix}
\)
確認:(2x2)型x(2x3)型=(2x3)型 ⇒行列の積が成立する。
\(=
\begin{pmatrix}
3\cdot1+2\cdot2& 3\cdot2+2\cdot1& 3\cdot0+2\cdot-1\\
2\cdot1+1\cdot2& 2\cdot2+1\cdot1& 2\cdot0+1\cdot-1
\end{pmatrix}
\)
\(
=\begin{pmatrix}
7& 8& -2\\
4& 5& -1
\end{pmatrix}
\)
[前問の行列を入れ換えた積]
(2)
\(
\begin{pmatrix}
1& 2& 0\\
2& 1& -1
\end{pmatrix}
\)
\(
\begin{pmatrix}
3& 2\\
2& 1
\end{pmatrix}
\)
確認:(2x3)型 (2x2)型⇒行列の積が成立しません。
∵前の行列の列(3)と後の行列の行(2)が一致していない。
(3)A B=
\((a_1\ a_2\ a_3)\)
\(
\begin{pmatrix}
b_1 \\
b_2 \\
b_3
\end{pmatrix}
\)
確認:(1x
3)型x(3x
1)型=(1x1)型⇒行列の積が成立します。
\(= a_1 b_1 + a_2 b_2 + a_3 b_3\)
[前問の行列を入れ換えた積]
(4)
\(B A=\)
\(
\begin{pmatrix}
b_1 \\
b_2 \\
b_3
\end{pmatrix}
\)
\((a_1\ a_2\ a_3)\)
確認:(3x
1)型x(1x
3)型=(3x3)型⇒行列の積が成立します。
\(=
\begin{pmatrix}
b_1 a_1& b_1 a_2& b_1 a_3 \\
b_2 a_1& b_2 a_2& b_2 a_3 \\
b_3 a_1& b_3 a_2& b_3 a_3
\end{pmatrix}
\)
[3つの行列の積の順番を変える]
(5)
\(A(BC)=(AB)C\)
を確認する。
\(A=
\begin{pmatrix}
1& 2\\
2& 1
\end{pmatrix}
\)
,
\(B=
\begin{pmatrix}
2& 1\\
4& 3
\end{pmatrix}
\)
,
\(C=
\begin{pmatrix}
1& 2\\
3& 4
\end{pmatrix}
\)
\(\underline{A(BC)}\):
\(BC=
\begin{pmatrix}
2& 1\\
4& 3
\end{pmatrix}
\)
\(
\begin{pmatrix}
1& 2\\
3& 4
\end{pmatrix}
\)
\(=
\begin{pmatrix}
5& 8\\
13& 20
\end{pmatrix}
\)
\(A(BC)=
\begin{pmatrix}
1& 2\\
2& 1
\end{pmatrix}
\)
\(
\begin{pmatrix}
5& 8\\
13& 20
\end{pmatrix}
\)
\(=
\begin{pmatrix}
31& 48\\
23& 36
\end{pmatrix}
\)
\(\underline{(AB)C}\):
\(AB
=
\begin{pmatrix}
1& 2\\
2& 1
\end{pmatrix}
\)
\(
\begin{pmatrix}
2& 1\\
4& 3
\end{pmatrix}
\)
=
\(
\begin{pmatrix}
10& 7\\
8& 5
\end{pmatrix}
\)
\( (AB)C=
\begin{pmatrix}
10& 7\\
8& 5
\end{pmatrix}
\)
\(
\begin{pmatrix}
1& 2\\
3& 4
\end{pmatrix}
\)
\(=
\underline{
\begin{pmatrix}
31& 48\\
23& 36
\end{pmatrix}
}
\)
[行列の交換をしたときの積]
(6)
\(AB \ne BA\)
を確認する。
行列A、Bは前問と同じとする。
\(AB\) は前問で計算済です。
\(AB=
\underline{
\begin{pmatrix}
10& 7\\
8& 5
\end{pmatrix}
}\)
\(BA=\)
\(\begin{pmatrix}
2& 1\\
4& 3
\end{pmatrix}
\)
\(\begin{pmatrix}
1& 2\\
2& 1
\end{pmatrix}\)
\(=
\underline{
\begin{pmatrix}
4& 5\\
10& 11
\end{pmatrix}
}\)
\(\therefore AB \ne BA\)
但し、単位行列、逆行列、対角行列との積は除く。(後述)
[ここまでのことより、行列の演算は実数などの四則演算は通用しない。]
5.行列の演算の性質1
\(A,B,C\):行列、
\(j,k\):スカラー(定数)として
(1)
行列の和とスカラー倍
(ⅰ)
\(A+B=B+A\)
(ⅱ)
\((A+B)+C=A+(B+C)\)
(ⅲ)
\((jk)A=j(kA)\)
(ⅳ)
\((j+k)A=jA+kA \)
(2)
行列の積及びその他
(ⅰ)\((AB)C=A(BC)\)
(ⅱ)
\(A(B+C)=AB+AC\)
(ⅲ)
\((A+B)C=AC+BC\)
(ⅳ)
\((kA)B=A(kB)=k(AB)\)
(ⅴ)
\(A=B \Leftrightarrow A_{i\ j}=B_{i\ j}\)
AとBの行列の型と各成分が等しいことを「相等」という。
これをもって
\(A=B\) であるという。
6.様々な行列
(1)
列ベクトルと行ベクトル
\(B=
\begin{pmatrix}
b_1 \\
b_2 \\
b_3
\end{pmatrix}
\)
:列ベクトル
\(A=(a_1\ a_2\ a_3)\)
:行ベクトル
この2つの積
\(B A=\)
は例題(4)を参照。
ここで突然「ベクトル」が登場したが、ベクトルを表す成分の数値なのか 単なる数値かだけの違いと考えてよい。
(2)
零行列
行列の成分が「0」である行列。
ゼロの「0」でなく大文字の「O」
\( O \)
\(=
\begin{pmatrix}
0& 0& 0\\
0& 0& 0\\
0& 0& 0
\end{pmatrix}
\)
(3)
対角行列
次の行列A は対角行列
対角成分以外は「0」の行列
\(A\)
\(=
\begin{pmatrix}
1& 0& 0\\
0& 2& 0\\
0& 0& 3
\end{pmatrix}
\)
主な特徴:積の演算が大変、簡単になる。
対角行列\(A=(a_{ij})\) と 行列\(B=(b_{ij})\)の積は:
\(AB\)
\(=
\begin{pmatrix}
1& 0& 0\\
0& 2& 0\\
0& 0& 3
\end{pmatrix}
\)
\(
\begin{pmatrix}
2& 3& 4\\
5& 6& 7\\
8& 9& 10
\end{pmatrix}
\)
\(=
\begin{pmatrix}
\color{red}{a_{11}b_{11}}& 0& 0\\
0& \color{red}{a_{22} b_{22}}& 0\\
0& 0& \color{red}{a_{33} b_{33}}
\end{pmatrix}
\)
\(=
\begin{pmatrix}
\color{red}{1\cdot 2}& 0& 0\\
0& \color{red}{2\cdot 6}& 0\\
0& 0& \color{red}{3\cdot 10}
\end{pmatrix}
\)
\(=
\begin{pmatrix}
\color{red}{2}& 0& 0\\
0& \color{red}{12}& 0\\
0& 0& \color{red}{30}
\end{pmatrix}
\)
(4)
単位行列
・対角行列の対角成分が「1」の行列。
・記号「E」か「I}が使われる。
\(E\)
\(=
\begin{pmatrix}
1& 0& 0\\
0& 1& 0\\
0& 0& 1
\end{pmatrix}
\)
(5)
正方行列とは
上記の対角行列、単位行列のように行と列の数が同じ行列。
\((m \times m)\)
型行列のこと。
7.行列の演算の性質2
対角行列\(A\) について
(ⅰ) \(AB=BA\)
単位行列\(E\) について
(ⅱ)\(EB=BE=B\)
零行列「O」について
(ⅲ)\(A+O=A\) \(,\quad (-A)+A=O\)
逆行列\(A^{-1}\)について
(ⅳ)
\(A^{-1} A=A A^{-1}=E \)
逆行列については先の講義で学びます。
【参照先】
ここまで次数を下げた行列を使い説明してきました。
最後に一般化した行列を書いておきます。
\((m \times n)\)型行列
\(
\begin{pmatrix}
a_{11} & a_{12} & \cdots& a_{1j}& \cdots & a_{1n}\\
a_{21} & \cdots & \cdots& a_{2j}& \cdots & a_{2n}\\
\vdots & \vdots & & \vdots& & \vdots\\
a_{i1} & a_{i2} & \cdots& a_{ij}& \cdots & a_{in}\\
\vdots & \vdots & & \vdots& & \vdots\\
a_{m1} & \cdots & \cdots& a_{mj}& \cdots & a_{mn}\\
\end{pmatrix}
\)
…以上