楽しく学ぶ…熱力学
マックスゥエルの速度分布
マックスゥエル登場。天才とは……。
マックスゥエル分布 マックスゥエルが初めて統計的手法を用いた。
1859年マックスゥエルは, クラウジウスの2本の論文と出会った。そして間違いを直感し, それまでギャンブルの道具とされていた, 確率と統計を柱とした理論を構築する。1860年「気体の力学的理論の例証」を発表し, 妻キャサリンと空気の粘性実験を行い, 理論の正しさを確証した。然し, 熱の正体を見事な形で説明した運動論も, 熱が熱い物体から冷たい物体へ自然に流れる理由は説明出来なかった。
淹れたてのコーヒーカップが熱く感じられるのは分かったが, 放っておくと冷める理由は分からないままだった。
第二法則が統計学と関係があるのは直感していたが, マックスゥエルの興味は電磁気に移ってしまった。
マックスウエルの速度分布 改めて速度と速さの違いに注意しよう。
これから説明するのは向きを持つ速度の分布である。
分子の\(~x~\)方向の速度\(~v_x~\)は, \(+~\)方向も\(~-~\)方向も同じだろうから平均速度は\(~\overline v_x=0~\)であろう。というのが速度である。
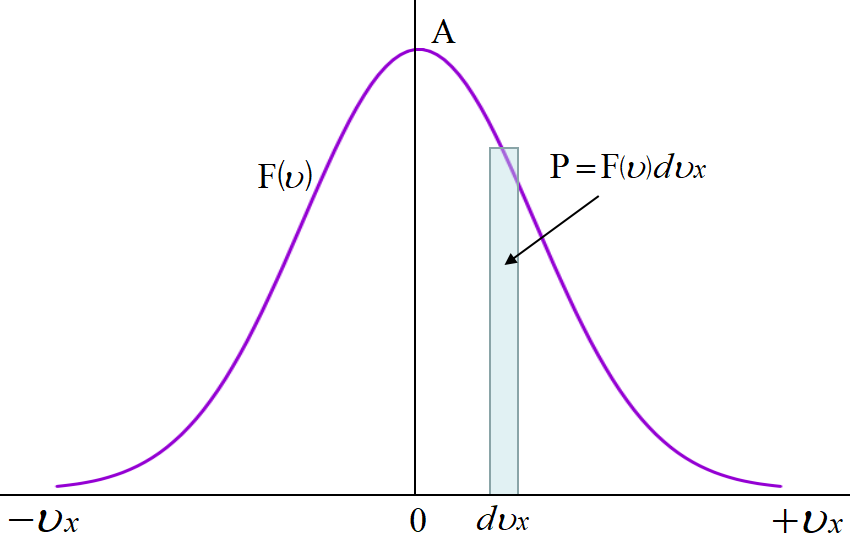
分子の\(~x~\)方向の速度が\(~v_x~\)くらいである確率を\(~P~\)とすれば,
\[P=f(v_x)dv_x \]
と表すことができる。
\(f(v_x)~\)は, その速度の分子がどれ位の割合で存在しているかを表しており
速度分布関数と呼ぶ。速度がちょうど\(~v_x~\)ということはないので,上式の正確な意味は, 速度が\(~v_x\sim v_x+dv_x~\)の間にある確率である。統計学では\(~f(v_x)~\)を
確率密度関数と呼ぶ。
全体で\(~N~\)個の分子があるとすれば,
\[Nf(v_x)dv_x \]
個の分子が, 速度\(~v_x\sim v_x+dv_x~\)までの間にある, ということである。
同じことは\(~y,z~\)方向についても言えるから, 速度が\(~(v_x,v_y,v_z)\sim (v_x+dv_x,v_y+dv_y,v_z+dv_z)~\)の間にある確率は,
\[P=f(v_x)dv_xf(v_y)dv_yf(v_z)dv_z \]
である。
この現象はどの方向も全く同等だろうから, 速度分布関数は方向に関係のない「速さ」\(~v~\)の関数として表せる形になっていなければならない。
\[P=F(v)dv_xdv_ydv_z \]
\(P~\)についての2つの式を比べて,
\[F(v)=f(v_x)f(v_y)f(v_z)\tag{1} \]
ここで「速さ」\(~v~\)は,
\[v^2=v_x^2+v_y^2+v_z^2\tag{2} \]
である。速さが2乗の形で表されているので, 改めて(1)式を,
\[F(v^2)=f(v_x^2)f(v_y^2)f(v_z^2)\tag{3} \]
と書き直す。ここで(2)式と(3)式をじっくり見比べよう。
(3) 式右辺は3つの式の積, 変数\(~v_x^2,v_y^2,v_z^2~\)の和が左辺\(~F(v^2)~\)の変数。
\(f(v_x^2),f(v_y^2),f(v_z^2)~\)は全く同じ形, \(F(v^2)~\)も恐らく同じような形。
こうなればもう指数関数しかない。そこで
\[f(v_x^2)=ae^{-bv_x^2},\;f(v_y^2)=ae^{-bv_y^2},\;f(v_z^2)=ae^{-bv_y^2} \]
とすれば,
\[\begin{align}
F(v^2)&=f(v_x^2)f(v_y^2)f(v_z^2)=a^3 e^{-b(v_x^2+v_y^2+v_z^2)}\\
&=Ae^{-bv^2}
\end{align} \]
となり, 期待通り\(f(v^2)~\)と\(~F(v^2)~\)が同じ形となっている。\(e~\)の肩を\(~-b~\)としたのは, この部分が正だと発散してしまうからである。
元々\(~v~\)だったものを無理やり\(~v^2~\)にしたので, 元に戻して自然な形にしておこう。
\[F(v)=f(v_x)f(v_y)f(v_z)=Ae^{-b(v_x^2+v_y^2+v_z^2)} \]
が求める, 分子の速度分布を表す関数である。
定数\(~A~\)と\(~b~\)は, 分子の総数が\(~N~\)個であることと, エネルギー(運動エネルギー)が\(~E~\)であることから決まる。
\[A\iiint_{-\infty}^{\infty}e^{-b(v_x^2+v_y^2+v_z^2)}dv_xdv_ydv_z=N \]
である。速度\(~v_x~\)は, 負も正もあるので, 積分は全範囲で行う。ガウス積分の公式
\[\int_{-\infty}^{\infty}e^{-\alpha x^2}dx=\sqrt{\frac{\pi}{\alpha}} \]
を使って,
\[A=\left(\frac{b}{\pi}\right)^{\frac{3}{2}}N \]
が得られる。\(N~\)個の分子のうち速度成分が\(~(v_x,v_y.v_z)~\)から\(~(v_x+dv_x,v_y+dv_y,v_z+dv_z)~\)
の間にある分子の数は,
\[N\left(\frac{b}{\pi}\right)^{\frac{3}{2}}e^{-(v_x^2+v_y^2+v_z^2)}dv_xdv_ydv_z \]
となる。
分子1個が\(\displaystyle \frac{1}{2}m(v_x^2+v_y^2+v_z^2)~\)の運動エネルギーを持っているので, 期待値を求める式,
\[E(X)=\int_{-\infty}^{\infty}X(x)f(x)dx \]
(\(E(X)~\)が期待値, \(X~\)は確率変数, \(f(x)~\)は\(X~\)の確率密度関数)を使って, 全運動エネルギーは,
\[E=\left(\frac{b}{\pi}\right)^{\frac{3}{2}}N\iiint_{-\infty}^{\infty} \frac{1}{2}m(v_x^2+v_y^2+v_z^2)e^{-b(v_x^2+v_y^2+v_z^2)}dv_xdv_ydv_z \]
である。このままでは積分が難しいので, 極座標を使う。
\[v_x=vsin\theta cos\phi,\;v_y=vsin\theta sin\phi,\;v_z=vcos\theta \]
より,
\[v^2=v_x^2+v_y^2+v_z^2,\;dv_xdv_ydv_z=4\pi v^2dv \]
を用いて
\[\begin{align}
E&=\left(\frac{b}{\pi}\right)^{\frac{3}{2}}\frac{m}{2}N\int_{0}^{\infty}v^2 e^{-bv^2}4\pi v^2dv \\
&=2\pi m\left(\frac{b}{\pi}\right)^{\frac{3}{2}}\frac{3}{8}\frac{\sqrt{\pi}}{b^{5/2}}N\\
&=\frac{3m}{4b}N
\end{align}\]
ここでガウス積分の公式
\[\int_{0}^{\infty}x^4e^{-\alpha x^2}dx=\frac{3}{8}\frac{\sqrt{\pi}}{\alpha^{5/2}} \]
を用いた。1モルの気体の内部エネルギーは
\[E=\frac{3}{2}RT \]
だったから,
\[\begin{align}
RT&=\frac{mN_A}{2b} \\
b&=\frac{m}{2}\frac{1}{kT}
\end{align} \]
を得る。結局\(N~\)個の分子のうち速度成分が\(~(v_x,v_y,v_z)~\)から\(~(v_x+dv_x,v_y+dv_y,v_z+dv_z)~\)の間にある分子の数は,
\[F(v_x,v_y,v_z)dv_xdv_ydv_z=N\left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}}e^{-\frac{m}{2kT}(v_x^2+v_y^2+v_z^2)}dv_xdv_ydv_z\tag{4} \]
となる。これが「マックスゥエルの速度分布関数」で, 次の「マックスゥエルの速さの分布」の基礎となる式である。
ところでこれは正規分布である。筆者の経験では, 正規分布は2項分布の極限操作で得られた。(4)式導出まで極限操作は入っていない。
しかし, 暗黙に行っているのである。それは「\(~y,z~\)方向も同じだろうからから」の部分である。同じだろうとは十分時間が経っていることである。\(N~\)個の分子が1か所から放たれた直後は\(~x,y,z~\)方向はすべて異なる。十分時間が経つと(とは言っても日常感覚では瞬間であろうが), 2項分布が崩れて正規分布となったわけである。(あまり見かけない説明で多少の不安はあるが)
マックスウエルの速さの分布 こちらが有名なマックスウエル分布である。
速度分布関数(4)を簡略化して書けば
\[F(v)=Ae^{-\alpha v^2}\tag{5} \]
である。
(5)式は静止している分子が最も多いことを示すものではない。\(F(v)~\)は統計学では
確率密度関数と呼ぶ。
\(F(v)dv~\)つまりグラフの微小面積がその範囲に粒子が存在する確率を与えるということである。
偏差値を考えれば分かるだろうか?多数の生徒から無作為に選べば, その生徒の偏差値は\(~50~\)近辺である確率が最も高い。正確に\(~50.00~\)である場合は殆んどなく, 例えば偏差値の幅を\(~4~\)とすれば, \(48\sim 52~\)の間の生徒が最も多い, といった具合である。
しかし我々の先入観では静止している分子は無く, 殆んどは音速を超えるスピードで運動している。先入観の静止は\(~v^2=v_x^2+v_y^2+v_z^2=0~\)つまり\(~(v_x,v_y,v_z)=(0,0,0)~\)のことで, 確かに殆んどあり得ない状態である。
\(~v^2=1~\)となると, \(~(v_x,v_y,v_z)=(1,0,0)~\)ばかりではなく, \((0,1,0)~\)も\((1/\sqrt{2} ,1/\sqrt{2},0)~\)も可能で, 無数にあり, \(v^2=1~\)である状態は格段に多い。
それでは速さ\(~v~\)を持つ粒子の個数はどのようにして求めたら良いのだろうか?
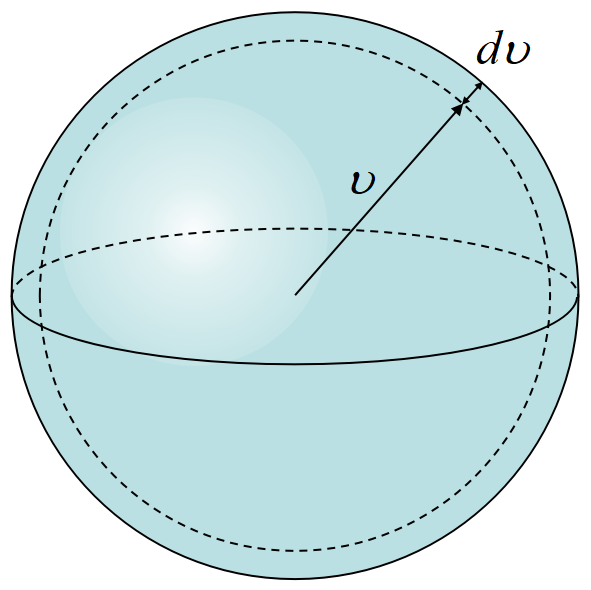
先ほどの\(~v^2=1~\)は, \((v_x,v_y,v_z)~\)空間で半径\(\;=1~\)の球面上の点である。ならば半径\(~v~\)の球面上の点の数が求める粒子数だろうか?
点の数といっても無限個あるわけだから数えるわけにはいかないが, 半径\(\;=1~\)と半径\(\;=2~\)では後者が4倍であろう。
球面上で1つの状態の占める面積が有限ならば…と量子論創成期のようなことが頭に浮かぶが, ただの思い付きだ。
話が少々混乱してきた。無限数の問題はあるが, 速さ\(~v~\)の状態数\(~W(v)~\)は球面の表面積\(~4\pi v^2~\)に比例するとしよう。
\[W(v)=K\x 4\pi v^2\tag{6} \]
すると速度が(速度と速さを厳密に使い分けているので注意!)\(~v\sim v+dv~\)の範囲の分子数は
\[N\x 4\pi Kv^2 F(v)dv\]
である。\(N~\)は総分子数, \(F(v)~\)は(5)式の\(~F(v)~\)である。(6)式の\(~K~\)は
\[\int_{0}^{\infty}N\x 4\pi Kv^2 F(v)dv=\int_{0}^{\infty}N\x 4\pi Kv^2 Ae^{-\alpha v^2}dv =N \tag{7} \]
より求められる。速さは\(~v\gt 0~\)なので積分は正の範囲で行う。ガウス積分公式
\[\int_{0}^{\infty}x^2e^{-\alpha x^2}=\frac{1}{4}\sqrt{\frac{\pi}{\alpha^3}} \]
を使うと, (7)式は
\[4\pi KA\int_{0}^{\infty}v^2e^{-\alpha v^2}dv=4\pi KA\frac{1}{4}\left(\frac{\pi}{\alpha ^3}\right)^{\frac{1}{2}}=1\]
ここで\(~\alpha=m/2kT~\)および(4)式の
\(\displaystyle A=\left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}}=\left(\frac{\alpha}{\pi}\right)^{\frac{3}{2}} \)
を使うと,
\[4\pi KA\frac{1}{4}\left(\frac{\pi}{\alpha ^3}\right)^{\frac{1}{2}}=4\pi K \left(\frac{\alpha}{\pi}\right)^{\frac{3}{2}}\frac{1}{4}\left(\frac{\pi}{\alpha ^3}\right)^{\frac{1}{2}} =1\]
より,
\[K=1\]
随分と簡単になった。ここで改めて,
\[\begin{align}
G(v)dv&=4\pi v^2F(v)dv \\
&=4\pi \left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}}v^2 e^{-\frac{m}{2kT}v^2}dv
\end{align} \]
とおけば, \(G(v)dv~\)は速度ベクトルの方向に関係なく, 速さが\(~v\sim v+dv~\)の範囲にある分子の割合(確率)を表す。
\(G(v)~\)がマックスゥエルの速さ分布関数(一般にはこちらを速度分布関数と呼ぶ様である.)である。
ところで\(~4\pi v^2dv~\)は, 半径\(~v~\), 厚さ\(~dv~\)の球殻であり, 速度空間\((v_x,v_y,v_z)~\)を定義すれば, その空間の微小要素である。
速度分布\(~F(v_x)~\)の場合は, \(N~\)個の分子のうち, 空間微小要素\(~dv_x~\)との積\(~NF(v_x)dv_x~\)が\(~v_x\sim v_x+dv_x~\)の範囲にある粒子数を表すのであった。
速さ分布\(~G(v)~\)の場合は, \(N~\)個の分子のうち, 空間微小要素\(~4\pi v^2dv~\)との積\(~ NF(v)4\pi v^2dv~\)が, \(~v\sim v+dv~\)の範囲にある粒子数を表すと考えればよい。つまり, 速さ分布関数は
\[G(v)=4\pi \left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}}v^2 e^{-\frac{m}{2kT}v^2}\tag{8} \]
である, とした方がスマートである。教科書もこの説明の方が多い。ヤコビアンを使ったさらに洗練された手法もある。
ただ凡才としてはいきなり速度空間だヤコビアンだと言われても…。
改めて, 速さが\(~v\sim v+dv~\)である粒子の個数は,
\[NG(v)4\pi v^2dv=4\pi N\left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}}v^2e^{-\frac{1}{2kT}mv^2}dv \]
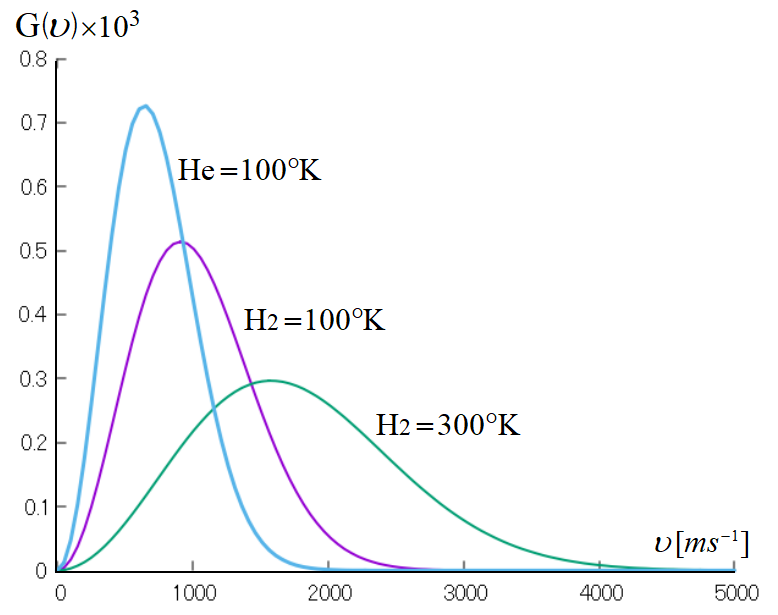
となる。下図は(8)式を図示したものである。縦軸は速さではなく, 確率密度であることに注意。
\(100\rm°K~\)で見ると, 重い原子の方が分布は急峻である。また軽い原子の方が速さは速い。\(100\rm°K~\)と\(~300\rm°K~\)を比べると, 温度が高い方が分布の幅が大きく, また速い原子の数も多い。
圧力・温度・エネルギー 基本的な考えは高校物理と同じ。
高校物理との違いは,
(1) 衝突が壁\(~\rm A~\)ではなく, 分子ごとに微小面積\(~dS~\)を考える。
(2) 衝突時間を微小時間\(~dt~\)とし, 衝突は1回とする。
位である。まとめて書けば
\(x~\)軸に垂直な壁に小面積\(~dS~\)を考え, 微小体積\(~v_xdt\x dS~\)内の分子が微小時間\(~dt~\)の間に1回, 壁に弾性衝突する。
壁との力積の交換, その結果生ずる圧力と体積から状態方程式との対比, 分子の運動エネルギー等々全て同じである。
Stefan Boltsman の方法参照。ただしマックスゥエルの方法では微小体積内の分子数にも速さ分布関数を用いる。
気体分子運動論の問題点
分子運動論は, 温度, エントロピー, 体積等を変数とする熱力学に対立するものとして捉える向きも多い、
しかし, 実際は熱力学より歴史も長く, 対立というよりは, 互いに手を取り合いながら発展してきた。
このように歴史も長いが問題点も多々ある。例を上げよう。
気体分子同士の衝突は弾性衝突であろう。エネルギー保存則と運動量保存則とが同時に満足されるので, 衝突の前後で気体全体の性質にはなにも変化が生じない。例えば, はじめに気体の温度が異方的な場合には弾性衝突を何度繰り返しても温度の異方性が保持される。つまり温度むらが解消されずに非平衡状態のままである。また, もし壁との衝突が弾性衝突, 鏡面反射ならば, 衝突後の気体分子の運動エネルギーの異方性は保存され, やはり非平衡状態のままである。
この問題の解決方法の一つは, 壁を乱反射性とすることである。乱反射性の壁と弾性衝突すると, 衝突後の気体分子の運動方向は無秩序になる。そうすると, 衝突後の気体分子の運動エネルギーは統計平均としてどの方向成分に対しても同じになり, 気体の温度の等方性が保証される。
乱反射性の壁はヴィーン\(~(Wilhelm\;Carl\;Werner\;Otto\;Fritz\;Franz\;Wien,\;1864-1928年)~\)がヴィーンの変位則を導出した(1893年)際に用いた方法である。
しかしこれでも問題は解決しない。壁との熱平衡である。弾性衝突である限り, 壁はいつまでも冷たいままである。すると壁とは非弾性乱反射でなければならない。
非弾性乱反射の壁はキルヒホッフ\(~(Gustav\;Robert\; Kirchhoff\;1824-87)~\)年が黒体放射を議論した時に用いた。黒体が放射を吸収したり放出したりするために, 黒体と放射とは熱平衡に達することが出来た。
もう十分に複雑な問題になってしまった。本格的に対処するためには統計力学の助けを借りなければならないが, 気体の輸送係数, 有限の大きさの気体分子等更に多くの要素を盛り込む必要がある。
原子数が数十個のミクロなスケールから, 宇宙や星の内部というような巨大なスケールにまで, 温度, 熱, 圧力だけで十分な精度で自然を記述する熱力学は, 全く以って不思議である。